Основные понятия об алгебраическом уравнении

 

 

Рассмотрим алгебраическое уравнение n-й степени

 

,                           (1.3)

 

где коэффициенты – действительные числа, причем .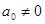

В общем случае будем считать, что  – комплексная переменная.

Теорема 1.1 (основная теорема алгебры). Алгебраическое уравнение n-й степени (1.3) имеет ровно n корней, действительных и комплексных, при условии, что каждый корень считается столько раз, какова его кратность.

При этом говорят, что корень  уравнения (1.3) имеет кратность s, если

 

, .

Комплексные корни уравнения (1.3) обладают свойством парной сопряженности.

Теорема 1.2. Если коэффициенты алгебраического уравнения (1.3) – действительные, то комплексные корни этого уравнения попарно комплексно-сопряженные, т.е. если  ( 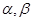– действительные числа) есть корень уравнения (1.3), кратности s, то число  также является корнем этого уравнения и имеет ту же кратность s.

Следствие. Алгебраическое уравнение нечетной степени с действительными коэффициентами имеет по меньшей мере один действительный корень.

 

Оценка границ модулей корней уравнения

 

 

Можно дать грубую оценку модулей корней уравнения (1.3)

Теорема 1.3. Пусть

 

,

 

где  – коэффициенты уравнения (1.3).

Тогда модули всех корней  (k=1,…,n) уравнения удовлетворяют неравенству

 

,                                               (1.4)

 

т.е. корни этого уравнения на комплексной плоскости  расположены внутри круга .

Следствие. Пусть  и . Тогда все корни  уравнения (1.3) удовлетворяют неравенству

 

,                                         (1.5)

т.е. корни уравнения (1.3) расположены в круговом кольце .