2020-01-14
142
Если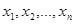 
– корни уравнения (1.3), то для левой части справедливо разложение
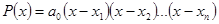. (1.6)
Произведя перемножение биномов в формуле (1.6) и приравнивая коэффициенты при одинаковых степенях x в левой и правой частях равенства (1.6), получим соотношения между корнями и коэффициентами алгебраического уравнения (1.3):
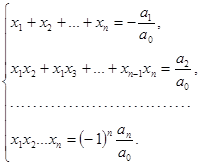(1.7)
Если учитывать кратности корней, то разложение (1.6) принимает вид
,
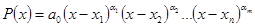где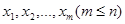 
–различные корни уравнения (1) и 
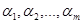– их кратности, причем 
.
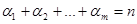Производная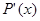 
выражается следующим образом:
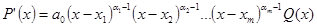
где Q(x) – полином такой, что
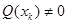при k=1,2,…,m
Поэтому полином
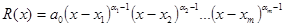
является наибольшим общим делителем полинома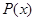 
и его производной 
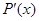, и может быть найден с помощью алгоритма Евклида [4]. Составим частное
,
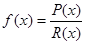и получим полином
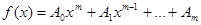
с действительными коэффициентами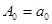 
, А1, A2,…, Am, корни которого 
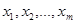различны.
Таким образом, решение алгебраического уравнения с кратными корнями сводится к решению алгебраического уравнения более низкого порядка с различными корнями.
|
|
|
Число корней полинома в некоторой области
Полное число корней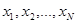 
уравнения 
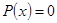, расположенных на комплексной плоскости внутри простого замкнутого контура Г, можно определить на основании следующей теоремы
Теорема 1.4. Если полином P(x) не имеет корней на замкнутом контуре Г, то число корней N этого полинома внутри контура Г в точности равно изменению Arg P(x) при положительном обходе контура Г, деленному на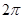 
, т.е.
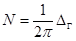Arg P(x),
причем каждый корень считается столько раз, какова его кратность.
Если уравнение контура Г есть
, 
,
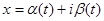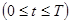где t – параметр, то для определения числа N на плоскости XOY строят кривую
, 
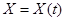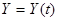
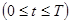, (1.8)
где
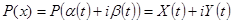
(X(t), Y(t) – действительные функции), и подсчитывают, сколько оборотов N делает кривая (1.9) делает вокруг начала координат.
