Основні властивості скалярного добутку

Скалярний добуток двох векторів

Скалярним добутком двох векторів і називається добуток довжин цих векторів на косинус кута, утвореного векторами, тобто

Тут символ означає кут між векторами. Нехай .

Тоді тобто скалярний добуток будь-якого вектора на одиничний вектор визначає величину проекції вектора на напрямок одиничного вектора.

Скалярний добуток двох векторів дорівнює добутку довжини одного з них на проекцію іншого на напрям першого.

Приклад. Під дією даної сили тіло перемістилося у даному напрямку на величину . Обчислити роботу сили (рис.2.12).

Рис.2.12

Р о з в ’ я з о к. Розкладемо силу на суму двох доданків: . Очевидно, робота суми сил дорівнює сумі складових сил. Але робота сили , перпендикулярної до напрямку шляху, дорівнює нулю, а робота сили , паралельної шляху, дорівнює добутку модуля сили на довжину шляху:

.

Але , тому остаточно одержимо

.

Скалярний добуток позначається одним з трьох способів:

.

Основні властивості скалярного добутку.

1⁰.

Якщо то Якщо то або або або а у нульового вектора напрям - довільний.

2⁰. - випливає зразу з означення.

3⁰.

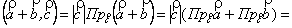
4⁰. .

Нехай Тоді

,

бо добутки взаємно перпендикулярних одиничних векторів дорівнюють нулю, а добутки паралельних однаково спрямованих одиничних векторів дорівнюють одиниці.

Отже,

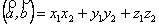, (2.9)

тобто дорівнює сумі добутків однойменних координат векторів.

Якщо , то з (2.9) маємо

(2.10)

Тому (2.11)

З формули (2.10) маємо . (2.12)

Формулами (2.10) і (2.12) визначаються відповідно квадрат довжини вектора і квадрат віддалі між точками і .

Якщо вектор -одиничний, то його проекціями на осі координат і відповідно є і . Тому з формули (2.11) маємо

. (2.13)

Оскільки , то

. (2.14)

Якщо у формулі (2.14) вектор ,то одержимо косинус кута, що його утворює вектор з віссю :

Аналогічно матимемо косинуси кутів і вектора з осями відповідно і :

Приклад. Визначити кут між векторами і , якщо вектор

перпендикулярний до вектора , а вектор перпендикулярний до вектора .

Р о з в ’ я з о к. Із перпендикулярності векторів і маємо

.

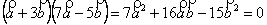Аналогічно .

Отже, маємо систему рівнянь:

Віднявши від першого рівняння друге, одержимо

Тоді

Отже,