Примеры вычисления математического ожидания случайной величины

38.1. Пусть гауссова случайная величина  имеет плотность распределения вероятностей (35.4). Вычислим ее математическое ожидание. Для этого подставим выражение (35.4) в формулу (37.4), тогда

    .               (38.1)

Вместо переменной интегрирования  введем новую переменную , , тогда

    .    (38.2)

Функция  является нечетной, поэтому интеграл в первом сла­гаемом (38.2) равен нулю. Во втором слагаемом

    .                                        (38.3)

Это равенство представляет собой условие нормировки для гауссовой плотности распределения вероятностей (35.4) с параметрами:  и . Таким об­разом, из (38.2) следует  - среднее гауссовой случайной величины является параметром плотности распределения вероятностей (35.4). В дан­ном случае  имеет геометрическую интерпретацию (рис. 35.2) как значе­ние аргумента , при котором плотность (35.4) принимает максимальное значение. В дальнейшем символ  используется также и для обозна­чения среднего любой случайной величины .

38.2. Вычислим среднее случайной величины , распределенной по экспоненциальному закону (35.8):

    .                               (38.4)

Далее используем способ интегрирования «по частям»:

    . (38.5)

38.3. Пусть  - число успехов в серии из  независимых опытов. Тогда вероятности ,  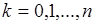определяются формулой Бер­нули. Поэтому

           .            (38.6)

Последнее равенство справедливо, поскольку 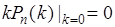. Подставим в (38.6) формулу Бернули, тогда:

. (38.7)

Введем новый индекс суммирования , тогда

    .             (38.8)

Поскольку 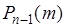 - вероятность  успехов в серии из  опытов, то  - как вероятность достоверного события, состоящего в появ­лении любого числа успехов в интервале . Поэтому из (38.8) следует

    .                                   (38.9)

38.4. Однако не у всякой случайной величины существует ее математи­ческое ожидание. Причиной этого является расходимость интеграла (37.4), что в свою очередь, обусловлено малой скоростью сходимости к нулю плот­ности  при , так что для функции  не существует интеграл вида (37.4). Для примера рассмотрим вычисление математического ожида­ния случайной величины , распределенной по закону Коши:     .

( 38.10)

Здесь несобственный интеграл расходится, так как

.

Следовательно, случайная величина  не имеет математического ожидания. Однако, если интеграл в (38.10) понимать в смысле главного значения Коши, то

,

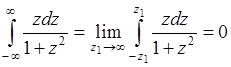 поскольку функция  является не­четной. Следовательно, при этом

    .                          (38.11)