35.1. Случайная величина 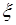 называется равномерно распределенной на отрезке
называется равномерно распределенной на отрезке  , если ее плотность распределения вероятностей
, если ее плотность распределения вероятностей
 (35.1)
(35.1)
где  - число, определяемое из условия нормировки:
- число, определяемое из условия нормировки:
 . (35.2)
. (35.2)
Подстановка (35.1) в (35.2) приводит к равенству, решение которого относительно  имеет вид:
имеет вид:  .
.
Функция распределения вероятностей 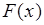 равномерно распределенной случайной величины может быть найдена по формуле (33.5), определяющей
равномерно распределенной случайной величины может быть найдена по формуле (33.5), определяющей  через плотность:
через плотность:
 (35.3)
(35.3)
На рис. 35.1 представлены графики функций  и
и  равномерно распределенной случайной величины.
равномерно распределенной случайной величины.

Рис. 35.1. Графики функции и плотности распределения
равномерно распределенной случайной величины.
35.2. Случайная величина 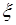 называется нормальной (или гауссовой), если ее плотность распределения вероятностей:
называется нормальной (или гауссовой), если ее плотность распределения вероятностей:
 , (35.4)
, (35.4)
где  ,
,  - числа, называемые параметрами функции
- числа, называемые параметрами функции  . При
. При  функция
функция  принимает свое максимальное значение:
принимает свое максимальное значение: 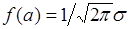 . Параметр
. Параметр  имеет смысл эффективной ширины
имеет смысл эффективной ширины  . Кроме этой геометрической интерпретации параметры
. Кроме этой геометрической интерпретации параметры  ,
, 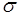 имеют и вероятностную трактовку, которая будет рассмотрена в последующем.
имеют и вероятностную трактовку, которая будет рассмотрена в последующем.
Из (35.4) следует выражение для функции распределения вероятностей
 , (35.5)
, (35.5)
где  - функция Лапласа. На рис. 35.2 представлены графики функций
- функция Лапласа. На рис. 35.2 представлены графики функций  и
и  нормальной случайной величины. Для обозначения того, что случайная величина
нормальной случайной величины. Для обозначения того, что случайная величина 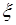 имеет нормальное распределение с параметрами
имеет нормальное распределение с параметрами  и
и  часто используется запись
часто используется запись  .
.

Рис. 35.2. Графики плотности и функции распределения
нормальной случайной величины.
35.3. Случайная величина 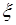 имеет плотность распределения вероятностей Коши, если
имеет плотность распределения вероятностей Коши, если
 . (35.6)
. (35.6)
Этой плотности соответствует функция распределения
 .
.
(35.7)
35.4. Случайная величина 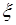 называется распределенной по экспоненциальному закону, если ее плотность распределения вероятностей имеет вид:
называется распределенной по экспоненциальному закону, если ее плотность распределения вероятностей имеет вид:
 (35.8)
(35.8)
Определим ее функцию распределения вероятностей. При  из (35.8) следует
из (35.8) следует  . Если
. Если  , то
, то
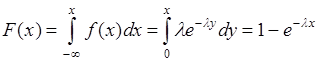 . (35.9)
. (35.9)
35.5. Релеевское распределение вероятностей случайной величины определяется плотностью вида
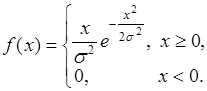 (35.10)
(35.10)
Этой плотности соответствует функция распределения вероятностей  при
при  и равная
и равная
 (35.11)
(35.11)
при  .
.
35.6. Рассмотрим примеры построения функции распределения и плотности дискретной случайной величины. Пусть случайная величина  - это число успехов в последовательности из
- это число успехов в последовательности из  независимых испытаний. Тогда случайная величина
независимых испытаний. Тогда случайная величина  принимает значения
принимает значения 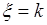 ,
,  с вероятностью
с вероятностью  , которая определяется формулой Бернулли:
, которая определяется формулой Бернулли:
 , (35.12)
, (35.12)
где  ,
, 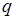 - вероятности успеха и неуспеха в одном опыте. Таким образом, функция распределения вероятностей случайной величины
- вероятности успеха и неуспеха в одном опыте. Таким образом, функция распределения вероятностей случайной величины  имеет вид
имеет вид
 , (35.13)
, (35.13)
где  - функция единичного скачка. Отсюда плотность распределения:
- функция единичного скачка. Отсюда плотность распределения:
 , (35.14)
, (35.14)
где  - дельта-функция.
- дельта-функция.
 2020-01-14
2020-01-14 122
122








