2020-01-14
66
Основные свойства математического ожидания следуют непосредственно из свойств интеграла в определении (37.5):
. (39.1)
1. Пусть 
представляет собой постоянную 
, тогда из (39.1) следует
, (39.2)
поскольку для плотности 
выполняется условие нормировки (33.6). Таким образом, математическое ожидание постоянной равно самой постоянной.
2. Пусть 
, где 
- число и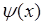 
- однозначная функция одной переменной, тогда из (39.1) следует
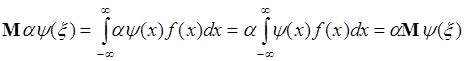. (39.3)
Таким образом, постоянный множитель 
можно вынести за знак математического ожидания.
3. Пусть 
, где 
- числа, 
- однозначные функции одной переменной, тогда из (39.1) следует
. (39.4)
Из этого равенства при 
следует свойство 2, а при 
и 
- свойство 1.
Математическое ожидание 
- это число, которое ставится в соответствие случайной величине 
. Поэтому 
можно рассматривать как операцию (оператор, функцию) над случайной величиной 
. В соответствии со свойствами 1-3 оператор математического ожидания является линейным оператором.
|
|
|
