| Интервальный ряд для Х 1 | ||
| Х 1 | F 1 | Ср. цена тыс.руб. |
| 0-1 | 21 | 603 |
| 1-2 | 14 | 554 |
| 2-3 | 7 | 522 |
| 3-4 | 4 | 420 |
| 4-5 | 2 | 414 |
| 5-6 | 1 | 379 |
| Интервальный ряд для Х 2 | ||
| Х 2 | F 2 | Ср. цена тыс.руб. |
| 0 - 21 | 25 | 601 |
| 21 - 42 | 9 | 551 |
| 42 - 63 | 7 | 490 |
| 63 - 84 | 2 | 420 |
| 84 - 105 | 4 | 466 |
| 105 - 126 | 2 | 417 |
| Интервальный ряд для Y | ||
| Y | F y | Ср. цена тыс.руб. |
| 379 - 422 | 4 | 400,5 |
| 422 - 465 | 5 | 443,5 |
| 465 - 508 | 4 | 486,5 |
| 508 - 551 | 8 | 529,5 |
| 551 - 594 | 12 | 572,5 |
| 594 - 637 | 6 | 615,5 |
| 637 - 683 | 10 | 660 |
Проведем аналитические группировки продаваемых автомобилей по времени эксплуатации и пробегу и определим групповые средние.
Построим график Y(X1)
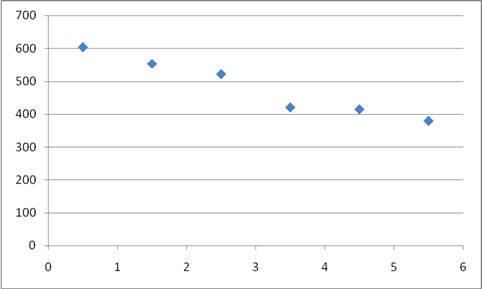
Зависимость цены от времени эксплуатации существует и носит линейный характер, чем больше время эксплуатации, тем дешевле автомобиль.
Построим график Y(X2)
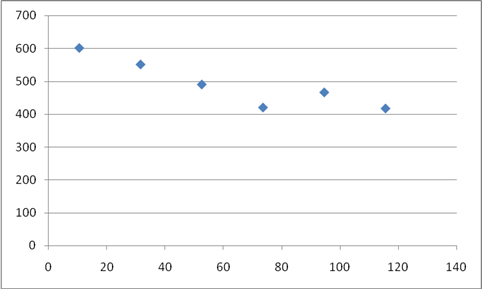
Зависимость цены от пробега существует и носит линейный характер, чем больше пробег автомобиля, тем дешевле автомобиль.
Группировка
На основании данных статистического наблюдения выделим три типа автомобилей:
· по времени эксплуатации:
o новые автомобили от 0 до 1 года – 34 шт.
o средние автомобили от 2 до 3 лет – 13 шт.
o старые автомобили от 3 до 5 лет – 3 шт.
· по пробегу:
o новые автомобили от 0 до 50 тыс. км. – 36 шт.
o средние автомобили от 50 до 100 тыс.км. – 11 шт.
o старые автомобили от 100 до 150 тыс.км. – 3 шт.
· по цене:
o новые автомобили от 581 до 683 тыс. руб. – 19 шт.
o средние автомобили от 480 до 581 тыс. руб. – 12 шт.
o старые автомобили от 379 до 480 тыс. руб. – 12 шт.
Определение доверительного интервала
Определим доверительный интервал, в котором заключена средняя цена всех продаваемых автомобилей, с вероятностью 0,9.
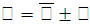
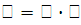
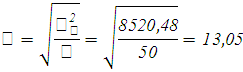
При вероятности 0,9 t = 1,64
Следовательно: 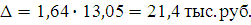
Таким образом, с вероятностью 0,9 можно утверждать, что средняя цена автомобиля равна:
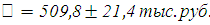
Определим доверительный интервал, в котором заключена средняя цена всех продаваемых автомобилей, с вероятностью 0,95.
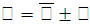
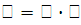
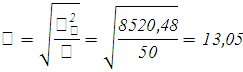
При вероятности 0,95 t = 1,96
Следовательно: 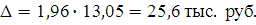
Таким образом, с вероятностью 0,95 можно утверждать, что средняя цена автомобиля равна:
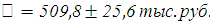
Определим необходимую численность выборки при определении средней цены продаваемых автомобилей, чтобы с вероятностью 0,95 предельная ошибка выборки не превышала 10 тыс. руб.
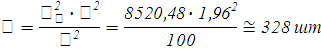
 2020-01-14
2020-01-14 129
129








