Проекциейточки А на заданную ось называется точка, которая является основание перпендикуляра, опущенного из точки А на ось.
Проекцию точки на ось можно также определить как точку пересечения оси с проектирующей плоскостью, т. е. с плоскостью, проведённой через данную точку перпендикулярно оси.
Пусть в пространстве заданы два вектора  и
и  .
.
Приведём их к общему началу. Углом между векторами  и
и 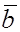 называется наименьший угол, на который надо повернуть один из векторов,
называется наименьший угол, на который надо повернуть один из векторов,
чтобы его направление совпало с направлением другого вектора. Из этого определения следует, что  .
.
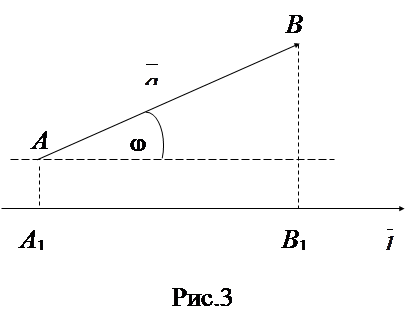 |
Пусть дан вектор
 и некоторая ось
и некоторая ось  . Опустим из точек
. Опустим из точек  и
и  перпендикуляры на ось
перпендикуляры на ось  и обозначим проекции этих точек на ось
и обозначим проекции этих точек на ось 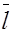 через
через  и
и  , соотвественно. Получим вспомогательный вектор
, соотвественно. Получим вспомогательный вектор  .
.
Определение 1.
Проекцией вектора  на ось
на ось 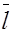 называется длина отрезка
называется длина отрезка  , взятая со знаком плюс, если вектор
, взятая со знаком плюс, если вектор  и ось
и ось 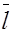 одинаково направлены, и со знаком минус, если они направлены в разные стороны.
одинаково направлены, и со знаком минус, если они направлены в разные стороны.
Проекцию вектора  на ось
на ось 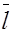 будем обозначать следующим образом:
будем обозначать следующим образом:  или
или  .
.
Очевидно, что  , если угол между векторами
, если угол между векторами  и
и 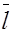 острый, и
острый, и 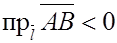 , если угол между векторами
, если угол между векторами  и
и 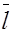 – тупой.
– тупой.
 2020-01-14
2020-01-14 178
178








