2020-01-14
343
Сумму двух векторов 
и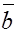 
можно найти по правилу параллелограмма.
Для этого надо привести их к общему началу и построить на этих векторах параллелограмм как на сторонах. Тогда диагональ параллелограмма, исходящая из общего начала векторов и 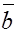и будет их суммой (рис.1).
.
Вычитание векторов можно выполнять
как сложение вектора и 
, т.е. 
.
Тогда вторая диагональ параллелограмма, исходящая из конца вектора 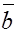даст нам вектор 
, представляющий собой разность векторов и :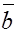 
.
Так как противоположные стороны параллелограмма равны и параллельны, то, учитывая определение равенства двух векторов, сумму векторов и 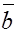можно представить как третий вектор 
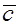, начало которого совпадает с началом вектора , а конец – с концом вектора .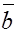
Такой способ построения суммы векторов называют правилом треугольника.
Для этого начало вектора 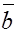надо совместить с концом вектора , а затем соединить начало вектора 
с концом вектора 
.
Тогда, как видно из рис.1, получим вектор .
