 ,
,
где 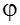 – угол наклона вектора
– угол наклона вектора  к оси
к оси  .
.
Теорема 1.
Проекция суммы двух векторов на ось равна сумме проекций слагаемых векторов на ту же ось.
Доказательство.
Пусть 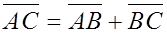 . Обозначим через
. Обозначим через  проекции на ось
проекции на ось 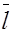 точек A, B и C соответственно. Пусть точки
точек A, B и C соответственно. Пусть точки  имеют по оси
имеют по оси  соответственно координаты
соответственно координаты  . Тогда
. Тогда
 ,
,  и
и 


 ,
,
что и требовалось доказать.
Эта теорема легко обобщается на случай любого числа слагаемых.
Теорема 2.
Если вектор  умножить на число
умножить на число  , то и его проекция на ось умножится на число
, то и его проекция на ось умножится на число  .
.
Доказательство.
Заметим, что если  , то вектор
, то вектор  направлен в ту же сторону, что и вектор
направлен в ту же сторону, что и вектор  и составляет с осью
и составляет с осью 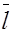 тот же угол
тот же угол 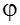 , что вектор
, что вектор  . Если
. Если  , то вектор
, то вектор  направлен противоположно вектору
направлен противоположно вектору  и составляет с осью
и составляет с осью 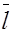 угол (
угол ( ).
).
1). Пусть  , тогда по формуле
, тогда по формуле
 .
.
2)пусть  , тогда по формуле
, тогда по формуле
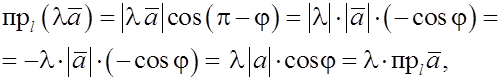
что и требовалось доказать.
Следствие.
Проекция разности двух векторов на ось 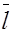 равна разности проекций этих векторов на ту же ось.
равна разности проекций этих векторов на ту же ось.
Произведение проекции вектора  на ось
на ось 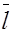 на единичный вектор этой оси (его называют ортом) называется составляющей вектора по оси
на единичный вектор этой оси (его называют ортом) называется составляющей вектора по оси  .
.
Координаты вектора в декартовом базисе
Определение 1.
Три некомпланарных вектора  ,
,  ,
,  называются правой тройкой векторов, если из конца третьего вектора (
называются правой тройкой векторов, если из конца третьего вектора (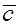 ) кратчайший поворот от первого вектора (
) кратчайший поворот от первого вектора (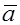 ) ко второму вектору (
) ко второму вектору ( ) виден происходящим в положительном направлении (против часовой стрелки) и левой тройкой в противном случае.
) виден происходящим в положительном направлении (против часовой стрелки) и левой тройкой в противном случае.
Мы уже говорили, что ортом ненулевого вектора 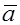 называется единичный вектор
называется единичный вектор  , направленный одинаково с вектором
, направленный одинаково с вектором  .
.
Выберем в пространстве произвольную точку  и проведём через неё три взаимно перпендикулярные оси. Перенумеруем их. Ось с выбранным на ней началом отсчёта и единицей длины называется координатной осью.
и проведём через неё три взаимно перпендикулярные оси. Перенумеруем их. Ось с выбранным на ней началом отсчёта и единицей длины называется координатной осью.
Упорядоченная система (т.е. перенумерованная система) трёх взаимно перпендикулярных координатных осей с общим началом отсчёта и общей единицей длины называется прямоугольной системой координат в пространстве (её называют также декартовой системой координат или ортогональной системой координат).
В этой системе координат первую ось будем называть осью абсцисс (или осью  ), вторую – осью ординат (или осью
), вторую – осью ординат (или осью  ), третью – осью аппликат (или осью
), третью – осью аппликат (или осью 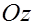 ).
).
Плоскости, содержащие любые две координатные оси будем называть координатными плоскостями:
плоскостью  или
или 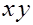 , если она содержит оси
, если она содержит оси  и
и  ,
,
плоскостью  или
или 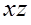 , если она содержит оси
, если она содержит оси  и
и 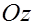 ,
,
плоскостью  или
или  , если она содержит оси
, если она содержит оси  и
и 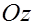 .
.
Эти плоскости будут перпендикулярны координатным осям 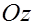 ,
,  и
и  соответственно.
соответственно.
Введём единичные векторы 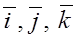 , направления которых совпадают с положительным направлением соответственно осей
, направления которых совпадают с положительным направлением соответственно осей  ,
,  ,
,  , т.е.
, т.е.
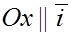 ,
,  ,
,  .
.
Векторы  в дальнейшем будем называть ортами осей прямоугольной или декартовой системы координат.
в дальнейшем будем называть ортами осей прямоугольной или декартовой системы координат.
Различают правую и левую координатные системы. В дальнейшем будем использовать правую систему координат.
Векторы  некомпланарны и, следовательно, образуют базис трёхмерного пространства. Эти векторы взаимно перпендикулярны и модули их равны единице
некомпланарны и, следовательно, образуют базис трёхмерного пространства. Эти векторы взаимно перпендикулярны и модули их равны единице
 .
.
Такая система базисных векторов называется ортогональной и нормированной.
Иногда говорят, что правая тройка взаимно ортогональных ортов 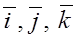 образует декартов базис.
образует декартов базис.
Рассмотрим произвольный вектор  и найдем проекции этого вектора на оси координат. Эти проекции будем называть координатами вектора
и найдем проекции этого вектора на оси координат. Эти проекции будем называть координатами вектора  в декартовом базисе
в декартовом базисе  .
.
Поместим начало вектора  в точку O. Тогда
в точку O. Тогда 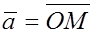 .
.
Проведем через конец вектора OM плоскости, параллельные координатным плоскостям. Они отсекут на координатных осях отрезки, которые представляют собой проекции вектора OM на соответствующие координатные оси. В результате такого построения получим прямоугольный параллелепипед, одной из диагоналей которого является вектор 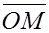 .
.
По правилу сложения векторов  ,
,
но  ,
,  .
.
Следовательно,
 |
 .
.
Рис.4
В правой части стоят составляющие вектора  по осям координат:
по осям координат:
 ,
,  ,
,
 ,
,
Тогда разложение вектора  по ортам декартовой системы координат запишется в виде
по ортам декартовой системы координат запишется в виде
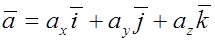 .
.
Часто используется более короткое обозначение  .
.
Зная проекции вектора  на координатные оси, можно легко найти
на координатные оси, можно легко найти  . Действительно, так как квадрат диагонали прямоугольного параллелепипеда равен сумме квадратов его сторон, то
. Действительно, так как квадрат диагонали прямоугольного параллелепипеда равен сумме квадратов его сторон, то 


 .
.
Вектор  (
( – начало координат) называется радиус-вектором точки M. Координатами
– начало координат) называется радиус-вектором точки M. Координатами  точки
точки 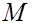 в пространстве называются проекции её радиуса-вектора
в пространстве называются проекции её радиуса-вектора  на координатные оси, т.е. координаты вектора
на координатные оси, т.е. координаты вектора  совпадают с координатами точки M
совпадают с координатами точки M
 .
.
Заметим, что радиус-вектор точки является связанным вектором, так как его начало всегда совпадает с началом координат.
Пусть  и
и  – точки пространства. Найдем координаты вектора
– точки пространства. Найдем координаты вектора  . По правилу сложения векторов имеем
. По правилу сложения векторов имеем
 ,
,


 .
.

Рис. 5
Таким образом, проекции вектора на координатные оси равны разностям соответствующих координат конца и начала вектора.
Теперь мы можем определить расстояние между двумя точками пространства как длину соответствующего вектора

Вспомним основные теоремы о проекциях. Пусть даны два вектора 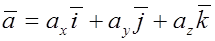 ,
,  и скаляр
и скаляр  . Тогда из свойств проекций вектора на ось следует
. Тогда из свойств проекций вектора на ось следует


Пусть  . Проектируя это равенство на оси координат, получим
. Проектируя это равенство на оси координат, получим  ,
,  ,
,  . Следовательно, одноимённые координаты у этих векторов пропорциональны
. Следовательно, одноимённые координаты у этих векторов пропорциональны
 .
.
Это условие коллинеарности векторов в координатной форме.
Косинусы углов, которые вектор  образует с осями координат, называются направляющими косинусами вектора
образует с осями координат, называются направляющими косинусами вектора  .
.
 ,
,
где  – угол между вектором
– угол между вектором  и осью
и осью  .
.
 ;
;  ;
;  ,
,
где  и
и  – углы между вектором
– углы между вектором  и осями
и осями  ,
,  и
и  соответственно.
соответственно.

 ,
,
таким образом,
 .
.
|
|
§6. Скалярное произведение двух векторов
Определение.
Скалярным произведением двух векторов  и
и  называется произведение их модулей на косинус угла между ними (т.е. число или скаляр):
называется произведение их модулей на косинус угла между ними (т.е. число или скаляр):
 .
.

Свойства скалярного произведения двух векторов:
1) Из определения следует переместительное свойство
 ;
;
2) Скалярное произведение равно нулю, т.е.
 или
или 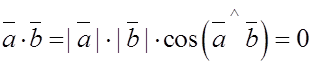
в двух следующих случаях:
а)  или
или 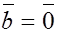
б) 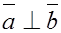 (ортогональны)
(ортогональны)
Таким образом, равенство нулю скалярного произведения двух векторов является необходимым и достаточным условием их перпендикулярности (или ортогональности)  .
.
3) Рассмотрим скалярное произведение двух коллинеарных векторов.
Если  , то
, то 
 . Если же
. Если же  , то мы имеем скалярное произведение вектора
, то мы имеем скалярное произведение вектора  самого на себя
самого на себя  .
.
Скалярное произведение вектора самого на себя называется скалярным квадратом и обозначается  .
.
4) Распределительное свойство
 .
.
 2020-01-14
2020-01-14 207
207








