Высшая Математика. (1 семестр).
Билет 1:
Вопрос 1:Прямоугольная и полярная системы координат:
Две взаимно перпендикулярные оси Ох и Оу с общим началом координат О и одинаковой масштабной единицей составляют прямоугольную (декартову) систему координатна плоскости Оху. Эти оси называются осями координат, ось Ох – осью абсцисс, ось Оу – осью ординат.

Разместим в пространстве координатную плоскость Оху так, чтобы ось ординат Оу лежала в плоскости чертежа и была направлена вправо, а ось Ох была направлена вниз и была перпендикулярна осям Оу и Оz. Из точки О – начала координат – перпендикулярно Оху вверх проведем ось Оz – ось аппликат. Если на всех осях взять одинаковую масштабную единицу, то получаем прямоугольную декартову систему координат в пространстве Охуz. Оси Ох, Оу, Оz называются координатными плоскостями.

Полярная система координат.
Проведем из точки О – полюса – луч, который является полярной осью.

Положение любой точки на плоскости определяется парой чисел. Угол  , на который нужно повернуть прямую О, чтобы она совпала с точкой М (поворот против чисовой стрелки). Полярный радиус – это длина отрезка ОМ.
, на который нужно повернуть прямую О, чтобы она совпала с точкой М (поворот против чисовой стрелки). Полярный радиус – это длина отрезка ОМ.
М ( ;
;  ), при этом 0
), при этом 0 

 2П, а 0
2П, а 0 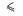

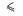 +
+  .
.
Совместим прямоугольную систему координат с полярной так, чтобы её начало совпадало с полюсом, а полярная ось - с осью абсцисс.
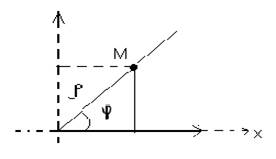
x =  cos
cos 
y =  sin
sin 
x2 +y2=  2(cos2
2(cos2  +sin2
+sin2  )
)



tg 


Вопрос 2: Определение предела функции:
Определение набора тех множеств, в которые последовательно, при своём изменении в соответствии с рассматриваемым условием, попадает переменное (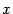 или
или  ), от которого зависит изменяющаяся величина (
), от которого зависит изменяющаяся величина ( или
или  ). В случае условия
). В случае условия  эти множества имеют вид
эти множества имеют вид  ; в случае
; в случае 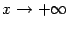 - вид
- вид 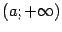 ; в случае
; в случае  - вид
- вид  . Назовём их окончаниями базы предела при данном условии, а полный набор таких окончаний - базой предела. Базу предела будем обозначать так же, как само условие, а именно,
. Назовём их окончаниями базы предела при данном условии, а полный набор таких окончаний - базой предела. Базу предела будем обозначать так же, как само условие, а именно,  ,
,  ,
,  и т. п.
и т. п.
Таким образом,


Итак, база предела - это набор окончаний, которые должны удовлетворять таким свойствам: все они непусты и если  и
и  - два разных окончания (одной и той же базы), то база должна содержать третье окончание
- два разных окончания (одной и той же базы), то база должна содержать третье окончание 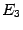 , которое содержится в каждом из первых двух:
, которое содержится в каждом из первых двух:  .
.
Определение: Пусть 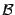 - некоторая база и функция
- некоторая база и функция  определена во всех точках
определена во всех точках 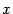 некоторого окончания
некоторого окончания 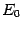 базы
базы 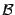 (и, значит, определена во всех точках более далёких окончаний
(и, значит, определена во всех точках более далёких окончаний  ). Число
). Число  называется пределом функции
называется пределом функции  по базе
по базе 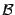 (или при базе
(или при базе 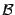 ) и обозначается
) и обозначается  если для любого (сколь угодно малого) числа
если для любого (сколь угодно малого) числа  найдётся такое окончание
найдётся такое окончание  базы
базы 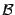 , что при всех
, что при всех  выполняется неравенство
выполняется неравенство  . Тот факт, что
. Тот факт, что  , записывают ещё в виде
, записывают ещё в виде 
Геометрический смысл данного определения предела таков: на плоскости  , на которой нарисован график функции
, на которой нарисован график функции 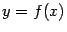 , проведём горизонтальную полосу ширины
, проведём горизонтальную полосу ширины  вокруг горизонтальной прямой
вокруг горизонтальной прямой  . Тот факт, что
. Тот факт, что  , означает, что найдётся достаточно далёкое окончание базы
, означает, что найдётся достаточно далёкое окончание базы 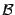 , на котором график функции целиком лежит в этой полосе. При уменьшении ширины полосы окончание, возможно, придётся брать более далёким, но, всё равно, и в любую более узкую полосу умещается график на достаточно далёком окончании.
, на котором график функции целиком лежит в этой полосе. При уменьшении ширины полосы окончание, возможно, придётся брать более далёким, но, всё равно, и в любую более узкую полосу умещается график на достаточно далёком окончании.
Билет 2:
Вопрос 1: Расстояние между двумя точками на плоскости и в пространстве:
1). Если точки на плоскости:
А(x1;y1) и В(x2;y2)

AB= 
2). Если точки в пространстве:
М(x1;y1;z1) и N(x2;y2;z2)
MN= 
Вопрос 2: Теоремы о пределах:
Теорема 1: Предел суммы двух функций равен сумме их пределов.



Распространяется на любое конечное число слагаемых и на алгебраическую сумму. Доказательство основывается на том, что если  , то f(x) можно записать как сумму предела и бесконечно малой величины. f(x)=a+ α(x), α(x) →0
, то f(x) можно записать как сумму предела и бесконечно малой величины. f(x)=a+ α(x), α(x) →0
Теорема 2: Постоянный множитель можно выносить за знак предела.

Теорема 3: предел произведения сомножителей равен произведению их пределов
Теорема 4: предел отношения двух функций, если предел  , равен отношению их пределов:
, равен отношению их пределов:

Билет 3:
 2020-01-14
2020-01-14 294
294







