Точки разрыва функции

Функция является непрерывной в точке, если  ó = .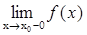

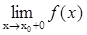
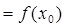Определение 1. Точки, в которых нарушается условие непрерывности, называют точками разрыва функции.

Определение 2. Точка разрыва х₀ называется точкой разрыва первого рода, если существуют односторонние конечные в этой точке.

Определение 3. Точка разрыва первого рода называется точкой устранимого разрыва, если односторонние пределы в этой точке равны.

Определение 4. Скачком функции в точке разрыва первого рода называется модуль разности односторонних пределов в этой точке.

Определение 5. Точка х₀ называется точкой разрыва второго рода, если она не является точкой разрыва первого рода (если хотя бы один из односторонних пределов не существует или равен +¥(-¥)).

Билет 4:

Вопрос 1: Определение вектора. Действия с векторами:

Определение вектора

Определение: Вектором называется направленный отрезок.

Вектор - это отрезок, у которого выделен один конец, называемый концом вектора. Этот конец на рисунке обозначается стрелкой. Другой конец отрезка называется началом вектора.

В математической литературе векторы обозначаются обычно одним из следующих способов: . В двух последних случаях - обозначение точки, являющейся началом вектора, 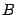- концом вектора.

 

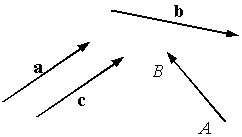
Рис.10.1.Изображение векторов

 

Определение: Два вектора называются равными, то есть не различаются как векторы, если соответствующие отрезки параллельны, имеют одинаковую длину и направление.

Определение: Векторы называются коллинеарными, если они параллельны одной прямой.

Определение: Векторы называются компланарными, если они параллельны одной плоскости.

Определение: Длиной или модулем вектора называется длина соответствующего направленного отрезка.

Модуль вектора a обозначается 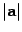. Вектор a называется единичным, если .

К множеству векторов необходимо добавить еще один объект, который мы будем называть нулевым вектором. Его можно рассматривать как отрезок, у которого начало и конец совпадают. Длина такого вектора равна нулю, направления он не имеет. Все нулевые векторы равны друг другу. Так как нулевой вектор лежит на любой прямой, то, по определению, он считается коллинеарным любому вектору и перпендикулярным любому вектору.

 

Действия с векторами

Определение: Суммой векторов a и b называется такой третий вектор c, что при совмещенных началах этих трех векторов, векторы a и b служат сторонами параллелограмма, а вектор c - его диагональю (рис. 10.2).

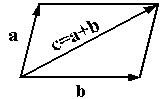
Рис.10.2.Сложение векторов

 

Сложение векторов в соответствии с рисунком 10.2 называется сложением по правилу параллелограмма. Однако бывает более удобным использовать для сложения правило треугольника, которое становится ясным из рисунка 1.3. Из того же рисунка видно, что результаты сложения по правилу параллелограмма и по правилу треугольника одинаковы.

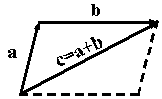
Рис.10.3.Правило треугольника

 

Определение: Вектор b называется противоположным вектору a, если a и b коллинеарные, имеют противоположные направления и .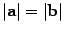

Вектор, противоположный вектору a, обозначается 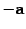, то есть .

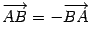Определение: Разностью векторов a и b называется сумма .

Разность обозначается 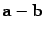, то есть .

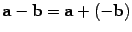Определение: Произведением вектора a на вещественное число 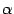называется вектор b, определяемый условием

1) 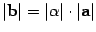и, если 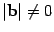, то еще двумя условиями:

2) вектор b коллинеарен вектору a;

3) векторы b и a направлены одинаково, если 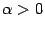, и противоположно, если .

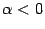Произведение вектора a на число 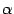обозначается 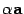(рис 1.4).

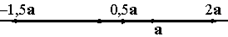
Рис.10.4.Умножение вектора на число

 

Замечание: Когда речь идет о связи векторов с числами, то иногда числа называют скалярами.

Теорема: Для любых векторов 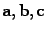и любых вещественных чисел выполняются следующие свойства:
1) (свойство коммутативности операции сложения);
2) 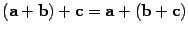(свойство ассоциативности операции сложения);
3) ;
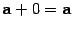4) ;
5) (свойство ассоциативности по отношению к числам);
6) 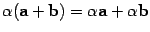(свойство дистрибутивности по отношению к умножению на число);
7) 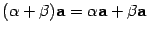(свойство дистрибутивности по отношению к умножению на вектор;
8) .

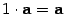9) равенство 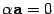верно тогда и только тогда, когда 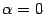или , или ;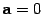
10) вектор, противоположный вектору a, равен 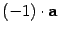, то есть ;
11) для любых векторов a и b существует такой вектор x, что .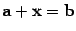

 

Вопрос 2: Бесконечно малые и бесконечно большие:

Бесконечно малые и их основные свойства:

Функция y=f(x) называется бесконечно малой при x→a или при x→∞, ес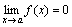ли или 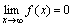, т.е. бесконечно малая функция – это функция, предел которой в данной точке равен нулю.

 

 

Теорема. Если функция y=f(x) представима при x→aв виде суммы постоянного числа b и бесконечно малой величины α(x): f (x)=b+ α(x) то .

Обратно, если , то f (x)=b+α(x), где a(x) – бесконечно малая при x→a.

Доказательство.

Докажем первую часть утверждения. Из равенства f(x)=b+α(x) следует |f(x) – b|=| α|. Но так как a(x) – бесконечно малая, то при произвольном ε найдется δ – окрестность точки a, при всех x из которой, значения a(x) удовлетворяют соотношению |α(x)|<ε. Тогда |f(x) – b|< ε. А это и значит, что .

Если , то при любом ε>0 для всех х из некоторой δ – окрестность точки a будет |f(x) – b|< ε. Но если обозначимf(x) – b= α, то |α(x)|<ε, а это значит, что a – бесконечно малая.

Рассмотрим основные свойства бесконечно малых функций.

Теорема 1. Алгебраическая сумма двух, трех и вообще любого конечного числа бесконечно малых есть функция бесконечно малая.

Доказательство. Приведем доказательство для двух слагаемых. Пусть f(x)=α(x)+β(x), где и 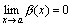. Нам нужно доказать, что при произвольном как угодно малом ε>0 найдется δ>0, такое, что для x, удовлетворяющих неравенству |x – a|<δ, выполняется |f(x)|< ε.

Итак, зафиксируем произвольное число ε>0. Так как по условию теоремы α(x) – бесконечно малая функция, то найдется такое δ1>0, что при |x – a|<δ1 имеем |α(x)|< ε/2. Аналогично, так как β(x) – бесконечно малая, то найдется такое δ2>0, что при |x – a|<δ2 имеем | β(x)|< ε/2.

Возьмем δ=min{ δ1, δ2}.Тогда в окрестности точки a радиуса δбудет выполняться каждое из неравенств |α(x)|< ε/2 и | β(x)|< ε/2. Следовательно, в этой окрестности будет

|f(x)|=| α(x)+β(x)| ≤ |α(x)| + | β(x)| < ε/2 + ε/2= ε,

т.е. |f(x)|<ε, что и требовалось доказать.

 

Теорема 2. Произведение бесконечно малой функции a(x) на ограниченную функцию f(x) при x→a (или при x→∞) есть бесконечно малая функция.

Доказательство. Так как функция f(x) ограничена, то существует число М такое, что при всех значениях x из некоторой окрестности точки a|f(x)|≤M. Кроме того, так как a(x) – бесконечно малая функция при x→a, то для произвольного ε>0 найдется окрестность точки a, в которой будет выполняться неравенство |α(x)|< ε/M. Тогда в меньшей из этих окрестностей имеем | αf|< ε/M= ε. А это и значит, что af – бесконечно малая. Для случая x→∞ доказательство проводится аналогично.

 

Из доказанной теоремы вытекают:

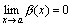Следствие 1. Если и , то .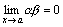

Следствие 2. Если и c=const, то .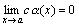

 

Теорема 3. Отношение бесконечно малой функции α(x) на функцию f(x), предел которой отличен от нуля, есть бесконечно малая функция.

Доказательство. Пусть 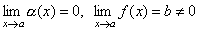. Тогда 1/f(x) есть ограниченная функция. Поэтому дробь 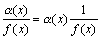есть произведение бесконечно малой функции на функцию ограниченную, т.е. функция бесконечно малая.