Определение. Векторным произведением векторов  и
и  называется вектор
называется вектор  , удовлетворяющий следующим условиям:
, удовлетворяющий следующим условиям:
1)  , где - угол между векторами
, где - угол между векторами  и
и  ,
, 
2) вектор  ортогонален векторам
ортогонален векторам  и
и 
3)  ,
,  и
и  образуют правую тройку векторов. Обозначается:
образуют правую тройку векторов. Обозначается:  или
или  . Свойства векторного произведения векторов:
. Свойства векторного произведения векторов:
1)  ;
;
2)  , если
, если 
 или
или  = 0 или
= 0 или  = 0;
= 0;
3) (m  )
)  =
=  (m
(m  ) = m(
) = m(
 );
);
4)  (
( +
+  ) =
) = 
 +
+ 
 ;
;
5) Если заданы векторы  (xa, ya, za) и
(xa, ya, za) и  (xb, yb, zb) в декартовой прямоугольной системе координат с единичными векторами
(xb, yb, zb) в декартовой прямоугольной системе координат с единичными векторами  , то
, то 
 =
= 
6) Геометрическим смыслом векторного произведения векторов является площадь параллелограмма, построенного на векторах  и
и  .
.
Пример. Найти векторное произведение векторов  и
и  .
.  = (2, 5, 1);
= (2, 5, 1);  = (1, 2, -3)
= (1, 2, -3)  .
.
Пример. Вычислить площадь треугольника с вершинами А(2, 2, 2), В(4, 0, 3), С(0, 1, 0). 


 (ед2).
(ед2).
Смешанное произведение векторов.
Определение. Смешанным произведением векторов  ,
,  и
и  называется число, равное скалярному произведению вектора
называется число, равное скалярному произведению вектора  на вектор, равный векторному произведению векторов
на вектор, равный векторному произведению векторов  и
и  . Обозначается
. Обозначается  или (
или ( ,
,  ,
,  ). Смешанное произведение
). Смешанное произведение  по модулю равно объему параллелепипеда, построенного на векторах
по модулю равно объему параллелепипеда, построенного на векторах  ,
,  и
и  .
.


Свойства смешанного произведения:
1)Смешанное произведение равно нулю, если: а)хоть один из векторов равен нулю; б)два из векторов коллинеарны; в)векторы компланарны.
2) 
3) 
4) 
5) Объем треугольной пирамиды, образованной векторами  ,
,  и
и  , равен
, равен 
6)Если  ,
,  , то
, то 
Пример. Доказать, что точки А(5; 7; 2), B(3; 1; -1), C(9; 4; -4), D(1; 5; 0) лежат в одной плоскости. Найдем координаты векторов:  Найдем смешанное произведение полученных векторов:
Найдем смешанное произведение полученных векторов:  , Таким образом, полученные выше векторы компланарны, следовательно точки A, B, C и D лежат в одной плоскости.
, Таким образом, полученные выше векторы компланарны, следовательно точки A, B, C и D лежат в одной плоскости.
Вопрос 2: Первый замечательный предел:
Определение: Первым замечательным пределом называется предел 
Теорема: Первый замечательный предел равен 

Доказательство. Рассмотрим два односторонних предела  и
и  и докажем, что каждый из них равен 1. Тогда по теореме двусторонний предел
и докажем, что каждый из них равен 1. Тогда по теореме двусторонний предел  также будет равняться 1.
также будет равняться 1.
Итак, пусть  (этот интервал - одно из окончаний базы
(этот интервал - одно из окончаний базы  ). В тригонометрическом круге (радиуса
). В тригонометрическом круге (радиуса  ) с центром
) с центром  построим центральный угол, равный
построим центральный угол, равный 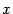 , и проведём вертикальную касательную в точке
, и проведём вертикальную касательную в точке  пересечения горизонтальной оси с окружностью (
пересечения горизонтальной оси с окружностью ( ). Обозначим точку пересечения луча с углом наклона
). Обозначим точку пересечения луча с углом наклона 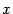 с окружностью буквой
с окружностью буквой  , а с вертикальной касательной -- буквой
, а с вертикальной касательной -- буквой  ; через
; через  обозначим проекцию точки
обозначим проекцию точки  на горизонтальную ось.
на горизонтальную ось.

Рис.2.27.Тригонометрический круг
Пусть  - площадь треугольника
- площадь треугольника  ,
,  - площадь кругового сектора
- площадь кругового сектора  , а
, а  - площадь треугольника
- площадь треугольника  . Тогда очевидно следующее неравенство:
. Тогда очевидно следующее неравенство:

Заметим, что горизонтальная координата точки  равна
равна  , а вертикальная -
, а вертикальная -  (это высота треугольника
(это высота треугольника  ), так что
), так что  . Площадь центрального сектора круга радиуса
. Площадь центрального сектора круга радиуса  с центральным углом
с центральным углом 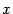 равна
равна  , так что
, так что  . Из треугольника
. Из треугольника  находим, что
находим, что  . Поэтому
. Поэтому  Неравенство, связывающее площади трёх фигур, можно теперь записать в виде
Неравенство, связывающее площади трёх фигур, можно теперь записать в виде

Все три части этого неравенства положительны, поэтому его можно записать так:

или (умножив на  ) так:
) так:

Предел постоянной 1 в правой части неравенства, очевидно, равен 1. Если мы покажем, что при  предел
предел  в левой части неравенства тоже равен 1, то по теореме "о двух милиционерах" предел средней части
в левой части неравенства тоже равен 1, то по теореме "о двух милиционерах" предел средней части  также будет равен 1.
также будет равен 1.
Итак, осталось доказать, что  . Сперва заметим, что
. Сперва заметим, что  , так как
, так как 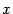 равняется длине дуги окружности
равняется длине дуги окружности  , которая, очевидно, длиннее хорды
, которая, очевидно, длиннее хорды  . Применяя теорему "о двух милиционерах" к неравенству
. Применяя теорему "о двух милиционерах" к неравенству

при  , получаем, что
, получаем, что
|
| (2.3) |
Простая замена переменной  показывает, что и
показывает, что и  . Теперь заметим, что
. Теперь заметим, что  . Применяя теоремы о линейности предела и о пределе произведения, получаем:
. Применяя теоремы о линейности предела и о пределе произведения, получаем:
|
| (2.4) |
Тем самым показано, что

Сделаем теперь замену  ; при этом база
; при этом база  перейдёт в базу
перейдёт в базу  (что означает, что если
(что означает, что если  , то
, то  ). Значит,
). Значит,

но  (
( -- нечётная функция), и поэтому
-- нечётная функция), и поэтому

Мы показали, что левосторонний предел также равен 1, что и завершает доказательство теоремы.
Доказанная теорема означает, что график функции  выглядит так:
выглядит так:

Рис.2.28.График 
Билет 7:
Вопрос 1: Уравнение плоскости. Вывод и исследование:
Пусть в трехмерном пространстве задана прямоугольная система координат. Попробуем установить, какой вид может иметь уравнение плоскости. Для этого заметим, что все плоскости, перпендикулярные одной прямой, параллельны друг другу.
Определение 1: Любая прямая, перпендикулярная плоскости, называется нормалью к плоскости, а любой ненулевой вектор на такой прямой мы будем называть нормальным вектором плоскости.
Замечание 1: Из определения видно, что нормальный вектор у фиксированной плоскости определяется не однозначно. Все нормальные векторы одной плоскости коллинеарны друг другу и поэтому получаются один из другого умножением на число, отличное от нуля.
Для того чтобы из параллельных плоскостей выбрать одну, достаточно задать точку, через которую проходит эта плоскость. Итак, если у плоскости известны нормальный вектор и точка, через которую она проходит, то плоскость определена однозначно.
Теорема 1: Пусть вектор  является нормальным вектором плоскости
является нормальным вектором плоскости  , проходящей через точку
, проходящей через точку  . Тогда уравнение
. Тогда уравнение
|
| (1) |
является уравнением плоскости  .
.
Доказательство. Пусть  -- некоторая точка плоскости
-- некоторая точка плоскости  (рис. 11.1). Иногда говорят "текущая точка" плоскости, так как предполагается, что ее координаты меняются и точка пробегает всю плоскость.
(рис. 11.1). Иногда говорят "текущая точка" плоскости, так как предполагается, что ее координаты меняются и точка пробегает всю плоскость.

Рис.11.1.
Вектор  лежит на плоскости
лежит на плоскости  . Следовательно, вектор
. Следовательно, вектор  ортогонален вектору n. Если же взять точку
ортогонален вектору n. Если же взять точку  , не лежащую на плоскости
, не лежащую на плоскости  , то вектор
, то вектор  не будет ортогональным вектору n. Так как условием ортогональности двух векторов является равенство нулю их скалярного произведения, то условием того, что точка
не будет ортогональным вектору n. Так как условием ортогональности двух векторов является равенство нулю их скалярного произведения, то условием того, что точка  лежит в плоскости
лежит в плоскости  , является выполнение равенства
, является выполнение равенства
|
| (2) |
Выразив скалярное произведение в левой части этого равенства через координаты сомножителей по формуле, получим формулу (1).
Пусть r -- радиус-вектор текущей точки  плоскости
плоскости  ,
,  -- радиус-вектор точки
-- радиус-вектор точки  . Тогда уравнение (2) можно переписать в виде
. Тогда уравнение (2) можно переписать в виде

Такое уравнение обычно называют векторным уравнением плоскости  .
.
Раскроем скобки в уравнении (1). Так как точка  - фиксированная, то выражение
- фиксированная, то выражение  является числом, которое обозначим буквой
является числом, которое обозначим буквой  . Тогда уравнение принимает вид
. Тогда уравнение принимает вид
|
| (3) |
Такое уравнение называется общим уравнением плоскости. Еще раз отметим, что в этом уравнении хотя бы один из коэффициентов  отличен от нуля, так как
отличен от нуля, так как  .
.
Верно и обратное утверждение:
Теорема 2: Всякое уравнение (3), в котором  , является уравнением плоскости, ортогональной вектору
, является уравнением плоскости, ортогональной вектору  .
.
Доказательство: Условие  означает, что хотя бы одно из чисел
означает, что хотя бы одно из чисел  , отлично от нуля. Пусть это будет, например, число
, отлично от нуля. Пусть это будет, например, число 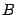 . Преобразуем уравнение (3) следующим образом:
. Преобразуем уравнение (3) следующим образом:

По теореме 1 такое уравнение является уравнением плоскости с нормальным вектором n, проходящей через точку  .
.
Теорема 3: позволяет написать уравнение плоскости, если известна точка этой плоскости и вектор, ортогональный плоскости. Однако, довольно часто встречаются задачи, где требуется получить уравнение плоскости, если известна точка, лежащая на ней, и два неколлинеарных вектора, лежащих или, что то же самое, параллельных плоскости. Покажем на примере, как решается такая задача.
Вопрос 2: Второй замечательный предел:
Определение: Вторым замечательным пределом называется предел

Число  , заданное этим пределом, играет очень большую роль как в математическом анализе, так и в других разделах математики. Число
, заданное этим пределом, играет очень большую роль как в математическом анализе, так и в других разделах математики. Число  часто называют основанием натуральных логарифмов.
часто называют основанием натуральных логарифмов.
Теорема: Второй замечательный предел существует. Его значение  - число, лежащее между
- число, лежащее между  и
и  .
.
Лемма: Пусть  и
и  - натуральное число. Тогда имеет место формула
- натуральное число. Тогда имеет место формула

Заметим, что в дроби  очевидно, сокращаются все сомножители в числителе и знаменателе, так что эта дробь равна 1. Аналогично, в предыдущем (не выписанном) слагаемом после сокращения получается коэффициент, равный
очевидно, сокращаются все сомножители в числителе и знаменателе, так что эта дробь равна 1. Аналогично, в предыдущем (не выписанном) слагаемом после сокращения получается коэффициент, равный  , в третьем справа слагаемом -равный
, в третьем справа слагаемом -равный  , и т. д. Таким образом, коэффициенты в слагаемых, стоящих на одинаковых местах, считая слева и справа от края формулы, совпадают.
, и т. д. Таким образом, коэффициенты в слагаемых, стоящих на одинаковых местах, считая слева и справа от края формулы, совпадают.
Доказательство. Оказывать утверждение леммы будем по индукции по параметру  . При
. При  формула, очевидно, верна:
формула, очевидно, верна:

Заметим, что при  и
и  ормула также хорошо известна:
ормула также хорошо известна:

и

Предположим, что она верна для  , и докажем, что тогда она верна и при
, и докажем, что тогда она верна и при  . Действительно,
. Действительно,

При этом в квадратных скобках получается:
|
|
|
|
|
|
|
|
|
и так далее, то есть как раз то, что должно получиться в качестве коэффициентов формулы бинома Ньютона при  .
.
Доказательство теоремы. Рассмотрим последовательность  и применим к
и применим к  формулу бинома Ньютона при
формулу бинома Ньютона при  и
и  . Получим
. Получим

Покажем, что последовательность  ограничена сверху. Для этого заменим все дроби
ограничена сверху. Для этого заменим все дроби  ,
,  ,...,
,...,  на 1. Все эти дроби меньше 1, так что сумма в правой части формулы увеличится:
на 1. Все эти дроби меньше 1, так что сумма в правой части формулы увеличится:

Далее, заменим все числа  в знаменателях этих слагаемых на 2; от этого правая часть ещё увеличится. Получим:
в знаменателях этих слагаемых на 2; от этого правая часть ещё увеличится. Получим:

В правой части получилась сумма членов геометрической прогрессии. Она равна

Поэтому

что и означает ограниченность последовательности сверху числом 3.
Покажем теперь, что последовательность  не убывает. Действительно, запишем формулу в виде
не убывает. Действительно, запишем формулу в виде

В аналогичной формуле, написанной для  вместо
вместо  , во-первых, увеличится каждое из выражений в круглых скобках (так как вычитаемое уменьшится) и, значит, увеличатся все слагаемые, содержащие такие скобки. Во-вторых, число слагаемых увеличится на одно: добавится положительное слагаемое
, во-первых, увеличится каждое из выражений в круглых скобках (так как вычитаемое уменьшится) и, значит, увеличатся все слагаемые, содержащие такие скобки. Во-вторых, число слагаемых увеличится на одно: добавится положительное слагаемое

Следовательно, при росте номера  члены последовательности
члены последовательности  строго возрастают:
строго возрастают:  при всех
при всех  .
.
Применим теперь к возрастающей ограниченной сверху последовательности  теорему о пределе монотонной ограниченной функции и получим, что существует предел
теорему о пределе монотонной ограниченной функции и получим, что существует предел

причём число  не больше постоянной 3, ограничивающей последовательность. Осталось заметить, что
не больше постоянной 3, ограничивающей последовательность. Осталось заметить, что  . Так как все последующие члены
. Так как все последующие члены  ещё больше, то и предел
ещё больше, то и предел  , на основании теоремы о переходе к пределу в неравенстве, не меньше числа
, на основании теоремы о переходе к пределу в неравенстве, не меньше числа  , что и завершает доказательство теоремы.
, что и завершает доказательство теоремы.
Замечание: Можно также показать, что
|
|
однако строгое доказательство достаточно тяжело, и мы его здесь пропускаем.
В формуле можно сделать замену  , при этом база
, при этом база 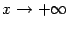 перейдёт в базу
перейдёт в базу  , и мы получим
, и мы получим

Билет 8:
Вопрос 1: Условия параллельности и перпендикулярности плоскостей:

|
Угол между двумя плоскостями в пространстве j связан с углом между нормалями к этим плоскостям j1 соотношением:
j = j1 или j = 1800 - j1, т.е. cos j =  cosj1.
cosj1.
Определим угол j1. Известно, что плоскости могут быть заданы соотношениями:
 , где
, где
 (A1, B1, C1),
(A1, B1, C1),  (A2, B2, C2). Угол между векторами нормали найдем из их скалярного произведения:
(A2, B2, C2). Угол между векторами нормали найдем из их скалярного произведения:
 .
.
Таким образом, угол между плоскостями находится по формуле:

Выбор знака косинуса зависит от того, какой угол между плоскостями следует найти – острый, или смежный с ним тупой.
На основе полученной выше формулы для нахождения угла между плоскостями можно найти условия параллельности и перпендикулярности плоскостей.
Для того, чтобы плоскости были перпендикулярны необходимо и достаточно, чтобы косинус угла между плоскостями равнялся нулю. Это условие выполняется, если:
 .
.
Плоскости параллельны, векторы нормалей коллинеарны:  //
//  .Это условие выполняется, если:
.Это условие выполняется, если:  .
.
Вопрос 2: Неопределенности и способы их раскрытия:
Раскрытие неопределённостей — методы вычисления пределов функций, заданных формулами, которые в результате формальной подстановки в них предельных значений аргумента теряют смысл, то есть переходят в выражения типа:
1.  ,
,
2.  ,
,
3. 0 / 0,
4. 00,
5.  ,
,
6.  ,
,
7. 
По таким выражениям сложно судить о том, существуют или нет искомые пределы, не говоря уже о нахождении их значений, если они существуют.
Правило Лопиталя: раскрытия неопределенностей 0/0 и ∞/∞
Ранее мы познакомились с примерами нахождения пределов отношения двух бесконечно малых или бесконечно больших функций, то есть раскрытия неопределенностей вида 0/0 и ∞/∞. Сейчас рассмотрим новое правило раскрытия этих неопределенностей.
Теорема (правило Лопиталя). Пусть функции f(x) и g(x) дифференцируемы в некоторой окрестности точки a, за исключением, быть может, самой точки a, и пусть  или
или  . Тогда, если существует предел отношения производных этих функций
. Тогда, если существует предел отношения производных этих функций  , то существует и предел отношения самих функций f(x)/g(x) при x→а, причем
, то существует и предел отношения самих функций f(x)/g(x) при x→а, причем

| (1) |
Таким образом, коротко правило Лопиталя можно сформулировать следующим образом: предел отношения двух бесконечно малых или двух бесконечно больших величин равен пределу отношения их производных.
Замечание. Отметим, что формула (1) справедлива только в том случае, если предел, стоящий справа, существует. Может случиться, что предел, стоящий слева существует, в то время как предел, стоящий в правой части равенства, не существует.
Билет 9:
Вопрос 1: Общее уравнение прямой на плоскости. Различные способы задания прямой:
Определение. Любая прямая на плоскости может быть задана уравнением первого порядка Ах + Ву + С = 0, причем постоянные А, В не равны нулю одновременно, т.е. А2 + В2 ¹ 0. Это уравнение первого порядка называют общим уравнением прямой. В зависимости от значений постоянных А,В и С возможны следующие частные случаи:- C = 0, А ¹ 0, В ¹ 0 – прямая проходит через начало координат- А = 0, В ¹ 0, С ¹ 0 { By + C = 0}- прямая параллельна оси Ох- В = 0, А ¹ 0, С ¹ 0 { Ax + C = 0} – прямая параллельна оси Оу- В = С = 0, А ¹ 0 – прямая совпадает с осью Оу- А = С = 0, В ¹ 0 – прямая совпадает с осью Ох Уравнение прямой может быть представлено в различном виде в зависимости от каких – либо заданных начальных условий.
 2020-01-14
2020-01-14 571
571

















