2020-01-14
138
Рассмотрим два произвольных вектора: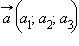 
и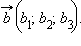 
Определение: Ненулевой вектор называется направляющим вектором прямой a, если он лежит либо на прямой a, либо на прямой, параллельной a.
Определение: Углом между ненулевыми векторами называется угол между прямыми, для которых данные вектора являются направляющими. Угол между любым вектором и нулевым вектором по определению считаем равным нулю. Если угол между векторами равен 90°, то такие вектора называются перпендикулярными. Угол между векторами будем обозначать так: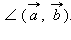 
Определение: Скалярным произведением векторов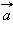 
и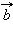 
называется произведение их длин на косинус угла между ними:
|
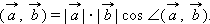
Совершенно аналогично, как в планиметрии, доказываются следующие утверждения:
Скалярное произведение двух ненулевых векторов равно нулю тогда и только тогда, когда эти векторы перпендикулярны.
Скалярный квадрат вектора, то есть скалярное произведение его самого на себя, равно квадрату его длины.
Скалярное произведение двух векторов 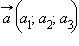и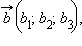 
заданных своими координатами, может быть вычислено по формуле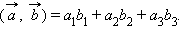 
Перечислим основные свойства скалярного произведения, которые также доказываются аналогично планиметрическим.
Для любых векторов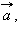 
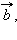и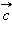 
и любого числа λ справедливы равенства:
1. 
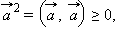причем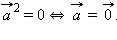 
2. 
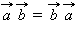(переместительный закон).
3. 
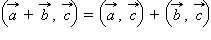(распределительный закон).
4. 
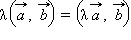(сочетательный закон).
Вопрос 2: Свойства непрерывных функций:
Свойства функций, непрерывных в точке
