Метод деления отрезка пополам для решения уравнений

         Речь по-прежнему идет об отыскании корней уравнения

,

т.е. таких чисел , что при подстановке в уравнение вместо симво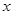ла числа  получается тождество. Само собой разумеется, что здесь, как и всюду в этом курсе, речь идет только о вещественных числах.

    О функции в приводимых ниже рассуждениях по-прежнему предполагается, что она обладает непрерывными производными тех порядков, которые упоминаются по ходу изложения.

    Напоминаем, отделить корень уравнения - это значит найти такой интервал (a,b), который, во-первых, содержит корень уравнения и, во-вторых, содержит только один корень этого уравнения. Доказывается, что если на концах некоторого интервала (a,b) функция  имеет разные знаки, а внутри этого интервала производная знак не меняет, то в интервале (a,b) корень уравнения есть и, притом, только один.

    Отсюда возникает простая методика приближенного поиска корня, отделенного в интервале (a,b): надо построить последовательность точек 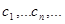по следующему правилу: затем из двух интервалов (a,c₁) и (c₁,b)­ выбирается тот, на концах которого  имеет разные знаки и его середина принимается за ; обозначим концы этого интервала (у которого - середина) через (a₂,b₂), а затем выберем ту из его половин, на концах которой имеет разные знаки. Пусть (a₃,b₃) - эта половина и  - середина этого отрезка и т.д. Доказывается, что построенная последовательность 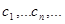 сходится к корню уравнения.

Если с самого начала задается некоторая точность вычислений, то на практике построение последовательности 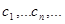 прерывается тогда, когда два раза подряд получаются одинаковые с заданной точностью числа. Это последнее перед прерыванием построения последовательности число и принимается за приближенное с заданной степенью точности значение корня.

    Описанный метод уточнения корня называется методом деления отрезка пополам.