При движении по гармонической неровности пути реактивные усилия  в симметричном вагоне вызывают колебания подпрыгивания и галопирования, которые описываются уравнениями (6.19):
в симметричном вагоне вызывают колебания подпрыгивания и галопирования, которые описываются уравнениями (6.19):
 (8.1)
(8.1)
 (8.2)
(8.2)
Уравнения (8.1) и (8.2) однотипны. Проследим решение одного из уравнений, например, колебания подпрыгивания. Другое будет решаться аналогично первому.
Общее решение уравнения (8.1) складывается из частного решения однородного уравнения (без первой части) и частного решения неоднородного уравнения (с правой частью):
 (8.3)
(8.3)
Частное решение  отвечает свободным колебаниям системы (рис.8.1,б), а частное решение
отвечает свободным колебаниям системы (рис.8.1,б), а частное решение  - вынужденным (рис. 8.1,а).
- вынужденным (рис. 8.1,а).
Произвольные постоянные 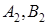 являются амплитудами свободных и вынужденных колебаний.
являются амплитудами свободных и вынужденных колебаний.
Если подставим частные производные 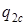 ,
,  соответственно в однородное и неоднородные уравнения, то найдем
соответственно в однородное и неоднородные уравнения, то найдем
 (8.4)
(8.4)
Общее решение (8.3) представится теперь в виде:
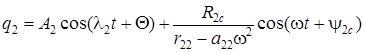 (8.5)
(8.5)
Возможны следующие случаи колебаний системы:
· нерезонансный, когда  ;
;
· резонансный, когда  ;
;
· случай близкий к резонансному,  .
.
Резонансным случаем (режимом) колебаний считают тот, когда различия между частотами составляет не более 15%.
Колебания в нерезонансной области
При отклонении вагона от положения статического равновесия на величину  , вагон совершает гармонические колебания, определяемые первым членом уравнения (8.5). При воздействии на вагон только возмущающих нагрузок вагон совершает гармонические колебания с частотой
, вагон совершает гармонические колебания, определяемые первым членом уравнения (8.5). При воздействии на вагон только возмущающих нагрузок вагон совершает гармонические колебания с частотой 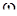 и амплитудой
и амплитудой  . Закон колебаний определяется вторым членом уравнения (8.5). В случае воздействия на вагон одновременно начальных возмущений
. Закон колебаний определяется вторым членом уравнения (8.5). В случае воздействия на вагон одновременно начальных возмущений  и возмущающих нагрузок
и возмущающих нагрузок  движения вагона определяются общим уравнением (8.5).
движения вагона определяются общим уравнением (8.5).
Из-за наличия в системе сил трения, свободные колебания с течением времени затухают и движение системы определяется вторым членом уравнения (8.5).
Колебания вагона в резонансном и близким к резонансу режимах
Считаем, что частоты возмущений близки к частоте свободных колебаний:
 (8.6)
(8.6)
где  – бесконечно малая величина.
– бесконечно малая величина.
Динамика вагона определяется законом движения (8.5) с учетом значений параметров (8.4).
Произвольные постоянные 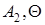 в решении (8.5) найдем из начальных условий движений системы. Полагаем, в начальный момент движения
в решении (8.5) найдем из начальных условий движений системы. Полагаем, в начальный момент движения  перемещение и скорость были равны нулю, то есть:
перемещение и скорость были равны нулю, то есть:
 (8.7)
(8.7)
Из решения системы (8.7) находим:
 (8.8)
(8.8)
Общее решение (8.5) с учетом (8.8) и последующим ее преобразованием через тригонометрические функции половинных углов принимает вид:
 (8.9)
(8.9)
Периоды тригонометрических функций равны:
 (8.10)
(8.10)

Рисунок 8.1 - График колебаний биения
Период  , поскольку
, поскольку  - бесконечно малая величина. Закон колебаний системы по условию (8.9) показан на рисунке 8.1. Колебания заданного вида называют колебаниями биения.
- бесконечно малая величина. Закон колебаний системы по условию (8.9) показан на рисунке 8.1. Колебания заданного вида называют колебаниями биения.
При более близком совпадении частот, в выражении (8.9) можно принять 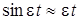 . Тогда закон колебаний подпрыгивания при учете значения (8.8) будет выражен функцией:
. Тогда закон колебаний подпрыгивания при учете значения (8.8) будет выражен функцией:
 (8.11)
(8.11)
Колебания пропорциональны времени  и нарастают с течением времени (рисунок 8.2).
и нарастают с течением времени (рисунок 8.2).


Рисунок 8.2 - График колебаний
За время одного цикла колебаний  происходит приращение амплитуд колебаний на величину:
происходит приращение амплитуд колебаний на величину:
 ,(8.12)
,(8.12)
Аналогично изложенному можно решить уравнение колебаний галопирования (8.2) и найти параметры колебаний:
 (8.13)
(8.13)
Выводы:
1. Колебания динамической системы без сил трения опасны тем, что в резонансном и околорезонансном режимах происходят значительные нарастания амплитуд колебаний. Возникает обезгрузка колесных пар и потеря их устойчивости против вкатывания на головку рельса. Возможны саморасцепы вагонов.
2. Уровень колебаний определяется величиной возмущающих нагрузок  , а последние соотношениями:
, а последние соотношениями:
· длины базы вагона и неровности пути;
· частот вынужденных  и свободных колебаний (
и свободных колебаний (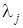 ).
).
3. Для снижения колебаний необходимо ввести в рессорное подвешивание диссипативные силы: вязкого или сухого трения.
 2020-01-14
2020-01-14 206
206








