Расчет параметров настройки непрерывных локальных систем управления

На рис. 4.1.1 показана математическая модель непрерывной системы управления с пе­редаточной функцией  и линейным управляющим устройством, реализую­щим ПИ-закон управления.

Здесь D x = x – x _зд — сигнал рассогласования, k _П — коэффициент передачи пропор­циональной части управляющего устройства, k _И — коэффициент передачи интегральной части управляющего устройства.

Рис. 4.1.1. Математическая модель непрерывной системы управления

Найдем передаточную функцию по каналу x _зд ® x:

.                                                                                                (1)

Отсюда имеем:

.                                                                                          (2)

Приведем передаточную функцию (2) к каноническому виду, разделив числитель и знаменатель на значение свободного члена k ₀ k _И.

В результате получим формулу:

,                                                                                                       (3)

где t = k _П/ k _И — время дифференцирования, T =  — постоянная времени, V = (1 + + k _П k ₀)  — степень демпфирования системы.

Передаточная функция (3) описывает динамические свойства данной системы управления. Статическая ошибка в этом случае равна нулю, поскольку значение переда­точной функции 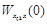 равно 1.

Действительно, x _уст = x (p) = x _зад = 1 · x _зад = x _зад. По этой причине D x _ст% = = 0. Время регулирования непрерывной системы управления можно оценить по соотно­шению:

t _р» 3 T /V.                                                                                                                                (4)

Подставляя в формулу (4) значения T =  и V = , получим:

t _р = 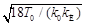.                                                                                                                  (5)

Для определения параметра настройки k _И воспользуемся соотношением:

t _р = .                                                                                                                                 (6)

Отсюда имеем: 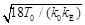 = , или:

 = .                                                                                                                   (7)

Формула (7) позволяет рассчитать значение параметра k _И, которое обеспечивает требуемое время регулирования. Значение второго параметра настройки k _П можно опре­делить из условия V = V^опт, где V^опт = 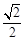 — оптимальная степень демпфирования системы. Этому значению (при t = 0) соответствует перерегулирование в пределах (3—5 %), что соответствует условиям настройки. В результате получаем соотношение:

V^опт = .                                                                                                                 (8)

Окончательно имеем:

.                                                                                                                    (9)

Рассчитаем требуемые значения коэффициентов k _П и k _И с помощью пакета MathСad.

Исходные данные для варианта № 2:

· постоянная времени объекта — T ₀ = 54 с;

· коэффициент усиления — k ₀ = 0,45;

· коэффициент l = 1,8;

Таким образом,  = l · T ₀ = 97,2 с.

Для определения параметра настройки 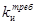 используем условие, что , где , то есть .

Время регулирования непрерывной системы управления можно оценить по соотношению . Следовательно, получаем соотношение: .

Зная, что , получаем .

Отсюда найдем значение параметра :

                                                                                                                 

Числовое значение параметра

1/с

                                                                                                

 

Из условия оптимальной переходной характеристики , где 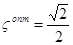 - оптимальная степень демпфирования, рассчитываем оптимальное значение параметра :

                                                                                                               (10)

             

 

 

 

В результате получаем следующую формулу:

                                                                                                     (11)

Числовое значение параметра

 

                                                                           (12)

Постоянная времени будет равна:

с

 

                                                                                       (13)

Время регулирования непрерывной системы управления:

с

 

                                                                                            (14)