Передаточная функция замкнутой системы равна:
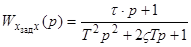 , где
, где  с. (1)
с. (1)
Примем, что входной сигнал xзад(t) имеет ступенчатый вид.
Аналитически входной сигнал описывается функцией:
xзад(t) = xзад(t)·1(t) (2)
Этой функции соответствует преобразование Лапласа:
Xзад(p) = xзад/p (3)
Найдем преобразования Лапласа для переходной характеристики:
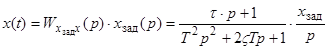 (4)
(4)
Переходную характеристику 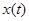 можно найти через обратное преобразование Лапласа:
можно найти через обратное преобразование Лапласа:
 (5)
(5)
или
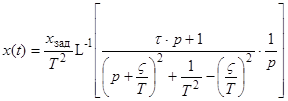 (6)
(6)
Введем обозначения:
|
|
|
|
(7)
|
|
|
|
(8)
При оптимальной настройке системы показатели α и ω0 должны совпадать.
Таким образом, выражение в квадратных скобах принимает вид:
 ; (9)
; (9)
Найдем числитель этой дроби:
 (10)
(10)
Получим систему уравнений:
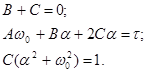
Решение системы имеет вид:
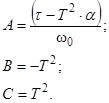
Тогда можно записать уравнение переходной характеристики:
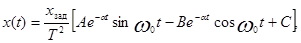 (11)
(11)
или
 где хзад = 1. (12)
где хзад = 1. (12)
График переходной характеристики непрерывной системы:
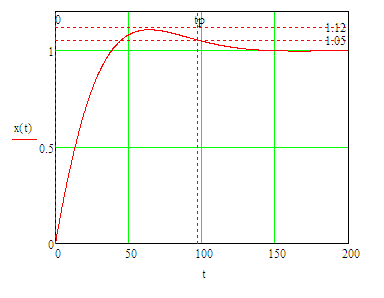
Рис. 4.2.1. График переходной характеристики х(t)
Определим по графику фактическое значение перерегулирования и время регулирования. Время регулирования определяется по моменту времени  , начиная с которого график переходной характеристики
, начиная с которого график переходной характеристики 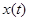 остается в заданном коридоре
остается в заданном коридоре 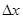 . Возьмем 0,05% значение коридора, т.е.
. Возьмем 0,05% значение коридора, т.е.
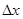 = 0,05.
= 0,05.
Максимальное значение, которого достигла переходная характеристика равно:
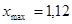 .
.
Таким образом, время регулирования равно:
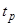 = 97.2 с;
= 97.2 с;
Значение перерегулирования равно:
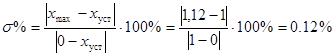 ; (13)
; (13)
при 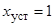 .
.
Величина статической ошибки рассчитывается по формуле:
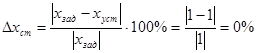 (14)
(14)
 2020-01-14
2020-01-14 153
153

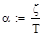
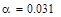 1/с
1/с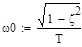
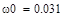 рад/с
рад/с






