Работая над проблемой зависимости в IA, Хансен [11] изобрел новую вычислительную модель, которая называется обобщенной интервальной арифметикой (GIA – generalized interval arithmetic). В этой модели, каждая входная переменная xi представлена интервалом, как в IA, и каждая промежуточная величина z, вычисленная в процессе оценки ¦(x1,…,xn) представлена как линейная комбинация входных переменных:
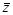 = z0 + z1x1+…+ znxn,
= z0 + z1x1+…+ znxn,
где каждый коэффициент zi сам является интервалом. Только коэффициенты zi записываются для каждой величины z; переменные xi подразумеваются. Т.о. GIA представляет величины многочленами первой степени с интервальными коэффициентами.
Как и в IA, для каждой элементарной операции или трансцендентной функции есть соответствующая GIA процедура, оперирующая этими обобщенными интервалами и возвращающая аналогичное представление для результата.
GIA модель следит за вкладом каждой входной переменной в окончательный результат и может использовать эту информацию для получения более точной оценки. Например, рассмотрим обобщенные интервалы
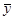 = [5, 7] x1 + [3, 4] x2,
= [5, 7] x1 + [3, 4] x2,
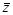 = [4, 6] x1 + [4, 5] x2,
= [4, 6] x1 + [4, 5] x2,
где переменные x1 и x2 имеют диапазоны [-10, 10]. Из этих данных мы можем вывести, что y и z содержатся в интервале [-110, 110]. В GIA модели разность 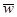 =
= 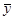 –
– 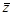 оценивается
оценивается
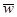 = [-1, 3] x1 + [-2, 0] x2 .
= [-1, 3] x1 + [-2, 0] x2 .
Это означает, что w находится в [-30, 30], в то время как IA дает [-220, 220].
Аффинная арифметика
Другая модель, применяемая к проблеме зависимости – аффинная арифметика (AA – affine arithmetic) [4]. В AA каждая величина x представлена аффинной формой
 = x0 + x1 e 1 + x2 e 2 + … + xn e n,
= x0 + x1 e 1 + x2 e 2 + … + xn e n,
где x0 – центр формы, xi (i = 1,.., n) – известные вещественные коэффициенты (записанные как числа с плавающей точкой), называемые частичными отклонениями, и e i – символьные переменные, называемые символами шума, чьи значения могут произвольно изменяться в интервале [-1, 1]. Т.о. AA поверхностно подобна GIA в том, что обе они представляют величины полиномами первой степени от символьных переменных. Тем не менее, как мы увидим ниже, число членов используемых в AA растет при выполнении вычисления, в то время как число членов используемых в GIA фиксировано и равно числу входных переменных.
Аффинные формы неявно представляют частичные зависимости между операндами: когда две аффинные формы совместно используют общие символы шума, величины, ими представленные, по крайней мере, частично зависят одна от другой. Как и в GIA, принятие таких зависимостей во внимание позволяет AA обеспечивать намного более точные оценки диапазонов, чем в IA, особенно в длинных вычислительных цепях. Другая основная польза, которая связана с этим, – то, что ошибка аффинного представления квадратично зависит от размера W, а не линейно.
AA используется в диапазонном анализе следующим образом. Вначале преобразовываем все входные интервалы к аффинным формам. Затем оперируем этими аффинными формами с помощью AA для вычисления желаемой функции. Окончательно, преобразовываем результат назад в интервал. Преобразования между IA и AA представлениями очевидны. Данный интервал 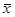 = [ a, b ] представляет некоторую величину x эквивалентной аффинной формой
= [ a, b ] представляет некоторую величину x эквивалентной аффинной формой  = x0 + xk e k , где x0 = (b+a) /2, xk = (b-a) /2. Поскольку входные интервалы обычно представляют независимые переменные, то для каждого входного интервала должен быть использован новый символ шума e k. Обратно, значение величины, представленной аффинной формой
= x0 + xk e k , где x0 = (b+a) /2, xk = (b-a) /2. Поскольку входные интервалы обычно представляют независимые переменные, то для каждого входного интервала должен быть использован новый символ шума e k. Обратно, значение величины, представленной аффинной формой  = x0 + x1 e 1 + x2 e 2 + … + xn e n, гарантированно будет лежать в интервале [ x0 - x, x0 + x ], где x = ||
= x0 + x1 e 1 + x2 e 2 + … + xn e n, гарантированно будет лежать в интервале [ x0 - x, x0 + x ], где x = ||  || = å| xi |. Заметим, что [ x0 - x, x0 + x ] – самый маленький интервал, содержащий все возможные значения
|| = å| xi |. Заметим, что [ x0 - x, x0 + x ] – самый маленький интервал, содержащий все возможные значения  , в предположении, что каждый e i изменяется независимо в интервале [-1, 1].
, в предположении, что каждый e i изменяется независимо в интервале [-1, 1].
Для оценки функции ¦ в AA, мы должны заменить каждую примитивную операцию Ф, которая появляется в выражении ¦ на эквивалентную операцию 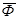 над аффинными формами, как это сделано в IA для интервалов. Для линейных операций z = Ф(x, y) соответствующая аффинная форма
над аффинными формами, как это сделано в IA для интервалов. Для линейных операций z = Ф(x, y) соответствующая аффинная форма 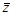 может быть выражена точно, как линейная комбинация символов шума, присутствующих в формах
может быть выражена точно, как линейная комбинация символов шума, присутствующих в формах 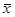 и
и 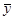 . Т.е. если
. Т.е. если
 = x0 + x1 e 1 + x2 e 2 + … + xn e n ,
= x0 + x1 e 1 + x2 e 2 + … + xn e n ,
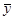 = y0 + y1 e 1 + y2 e 2 + … + yn e n , и a Î R, то:
= y0 + y1 e 1 + y2 e 2 + … + yn e n , и a Î R, то:
 ±
± 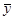 = (x0 ± y0) + (x1 ± y1) e 1 + (x2 ± y2) e 2 + … + (xn ± yn) e n ,
= (x0 ± y0) + (x1 ± y1) e 1 + (x2 ± y2) e 2 + … + (xn ± yn) e n ,
a  = (ax0) + (ax1) e 1 + (ax2) e 2 + … + (axn) e n ,
= (ax0) + (ax1) e 1 + (ax2) e 2 + … + (axn) e n ,
 ± a = (x0 + a) + x1 e 1 + x2 e 2 + … + xn e n
± a = (x0 + a) + x1 e 1 + x2 e 2 + … + xn e n
Заметим, что разность  –
–  равна 0, – полезное свойство, которое не верно в IA (или даже в GIA). Отсутствие таких тривиальных сокращений в IA является одним из источников взрыва ошибки.
равна 0, – полезное свойство, которое не верно в IA (или даже в GIA). Отсутствие таких тривиальных сокращений в IA является одним из источников взрыва ошибки.
Когда примитивная операция Ф нелинейна, значение 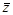 не может быть выражено непосредственно как линейная комбинация ei. В этом случае, мы подбираем хорошую линейную аппроксимацию для Ф (“хорошую” в чебышевском смысле минимизации максимальной ошибки), и добавляем дополнительный член zk ek для представления ошибки этой аппроксимации:
не может быть выражено непосредственно как линейная комбинация ei. В этом случае, мы подбираем хорошую линейную аппроксимацию для Ф (“хорошую” в чебышевском смысле минимизации максимальной ошибки), и добавляем дополнительный член zk ek для представления ошибки этой аппроксимации:
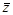 = z0 + z1 e 1 + z2 e 2 + … + zn e n + zk e k.
= z0 + z1 e 1 + z2 e 2 + … + zn e n + zk e k.
Здесь ek – новый шумовой символ и zk – верхняя граница ошибки аппроксимации. Выбор линейной аппроксимации должен принимать во внимание диапазоны операндов, которые подразумеваются аффинными формами  и
и 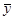 , и, возможно, также их взаимосвязь. Отметим, что в отличие от GIA, число членов, используемых в аффинных формах, растет во время оценки формулы. (При необходимости, лишние члены могут быть объединены и заменены новыми шумовыми символами ценою некоторой потери точности)
, и, возможно, также их взаимосвязь. Отметим, что в отличие от GIA, число членов, используемых в аффинных формах, растет во время оценки формулы. (При необходимости, лишние члены могут быть объединены и заменены новыми шумовыми символами ценою некоторой потери точности)
Важно заметить, что для дифференцируемой операции Ф граница ошибки z k хорошей чебышевской аппроксимации зависит квадратично от диапазонов операндов || 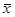 || и ||
|| и || 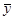 ||. Т.о., если функция ¦ использует только дифференцируемые операции, то различие между действительным диапазоном ¦ и диапазоном, вычисленном в AA стремится к нулю в относительном смысле при сужении области. Напротив, внутренние ошибки IA (следствие неучтенных взаимосвязей) зависят линейно от размеров области; поэтому различие будет уменьшаться только в абсолютном смысле.
||. Т.о., если функция ¦ использует только дифференцируемые операции, то различие между действительным диапазоном ¦ и диапазоном, вычисленном в AA стремится к нулю в относительном смысле при сужении области. Напротив, внутренние ошибки IA (следствие неучтенных взаимосвязей) зависят линейно от размеров области; поэтому различие будет уменьшаться только в абсолютном смысле.
Адекватные аппроксимационные алгоритмы были разработаны для основных арифметических операций и трансцендентных функций [5]. Например, при умножении двух аффинных форм 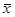 и
и 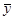 мы можем использовать аппроксимацию
мы можем использовать аппроксимацию
z0 = x0y0, zi = x0yi + y0xi, zk = ||  ||×||
||×|| 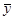 ||.
||.
Граница ошибки ||  ||×||
||×|| 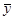 || не точна, а более чем в два раза больше максимальной ошибки. Для получения более точной границы, мы должны принять во внимание связь x и y, следующую из их аффинных форм, но еще не ясно, получим ли мы от этого выигрыш.
|| не точна, а более чем в два раза больше максимальной ошибки. Для получения более точной границы, мы должны принять во внимание связь x и y, следующую из их аффинных форм, но еще не ясно, получим ли мы от этого выигрыш.
Как описывалось применительно к IA, формулы для оценки примитивных функций в AA могут быть автоматически объединены в формулы для произвольно сложных функций. Этот факт и возможность преобразования позволяют AA просто заменить IA.
В качестве простого примера того, как AA обрабатывает проблему зависимости, рассмотрим оценку z = x(10 – x) в AA для x в интервале [4, 6]:
 = 5 + 1e1
= 5 + 1e1
10 –  = 5 - 1e1
= 5 - 1e1
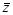 =
=  (10 –
(10 –  ) = 25 + 0e1 + 1e2
) = 25 + 0e1 + 1e2
[ 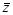 ] = [25 - 1, 25 + 1] = [24,26].
] = [25 - 1, 25 + 1] = [24,26].
Т.о. AA вычисляет оценку очень близкую к [24, 25] – действительному диапазону z. С другой стороны, IA оценка есть [16, 36]. Если выражение x (10 – x) раскрыто в 10 x – x 2, то IA оценка становится значительно хуже, [4, 44], в то время как оценка в AA точна – [24, 25].
 2020-01-14
2020-01-14 215
215








