Корреляционное отношение и индекс корреляции

Введенный выше коэффициент корреляции, как уже отмечено, является полноценным показателем тесноты связи лишь в случае линейной зависимости между переменными. Однако часто возникает необходимость в достоверном показателе интенсивности связи при любой форме зависимости.

Для получения такого показателя воспользуемся правилом сложения дисперсий:

                                                     (1.31)

где  общая дисперсия переменной

                                                           (1.32)

средняя групповых дисперсий , или остаточная дисперсия

                                                                  (1.33)

                                                            (1.34)

 межгрупповая дисперсия 

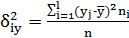                                                          (1.35).

Остаточной дисперсией измеряют ту часть колеблемости Y, которая возникает из-за изменчивости неучтенных факторов, не зависящих от Х. Межгрупповая дисперсия выражает ту часть вариации Y, которая обусловлена изменчивостью Х. Величина

                                                                   (1.36)

получила название эмпирического корреляционного отношения Yпо Х. Чем теснее связь, тем большее влияние на вариацию переменной Y оказывает изменчивость Х по сравнению с неучтенными факторами, тем выше .Величина ,называемая эмпирическим коэффициентом детерминации, показывает, какая часть общей вариации Y обусловлена вариацией Х. Аналогично вводится эмпирическое корреляционное отношение Х по Y:

                                                                   (1.37).

Отметим основные свойства корреляционных отношений:

1. Корреляционное отношение есть неотрицательная величина, не превосходящая единицу: 0 .

2. Если η=0, то корреляционная связь отсутствует.

3. Если η=1, то между переменными существует функциональная зависимость.

4. , т.е. в отличие от коэффициента корреляции r при вычислении корреляционного отношения существенно, какую переменную считать независимой, а какую– зависимой.

Эмпирическое корреляционное отношение  является показателем рассеяния точек корреляционного поля относительно эмпирической линии регрессии, выражаемой ломаной, соединяющей значения Однако в связи с тем, что закономерное изменение  нарушается случайными зигзагами ломаной, возникающими вследствие остаточного действия неучтенных факторов,  преувеличивает тесноту связи. По- этому наряду с  рассматривается показатель тесноты связи , характеризующий рассеяние точек корреляционного поля относительно линии регрессии  (1.3). Показатель  получил название теоретического корреляционного отношения или индекса корреляции Y по X:

                                                   (1.38).

Подобно  вводится и индекс корреляции X по Y:

                                                  (1.39).

Достоинством рассмотренных показателей η и R является то, что они могут быть вычислены при любой форме связи между переменными. Хотя η и завышает тесноту связи по сравнению с R, но для его вычисления не нужно знать уравнение регрессии. Корреляционные отношения η и R связаны с коэффициентом корреляции r следующим образом: 0

В случае линейной модели т.е. зависимости индекс корреляции  равен коэффициенту корреляции r(по абсолютной величине): .

  Коэффициент детерминации 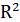, равный квадрату индекса корреляции (для парной линейной модели - r²), показывает долю общей вариации зависимой переменной, обусловленной регрессией или изменчивостью объясняющей переменной ..

Чем ближе 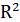  к единице, тем лучше регрессия аппроксимирует эмпирические данные, тем теснее наблюдения примыкают к линии регрессии. Если  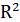 = 1, то эмпирические точки (x, у) лежат на линии регрессии (см. рис. 12.4) и между переменными Y и Х существует линейная функциональная зависимость. Если 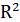=0, то вариация зависимой переменной полностью обусловлена воздействием неучтенных в модели переменных, и линия регрессии параллельна оси абсцисс.

 1.6 Понятие о многомерном корреляционном анализе.