Данные о статистической зависимости удобно задавать в виде корреляционной таблицы.
Рассмотрим в качестве примера зависимость между суточной выработкой продукции Y (т) и величиной основных производственных фондов Х (млн руб.) для совокупности 50 однотипных предприятий (табл. 1). 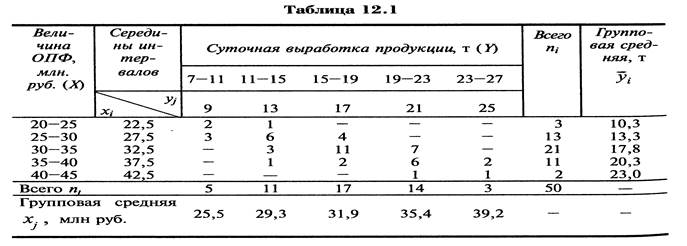 (В таблице через
(В таблице через 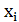 и
и  обозначены середины соответствующих интервалов, а через
обозначены середины соответствующих интервалов, а через 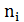 , и
, и 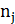 – соответственно их частоты.)
– соответственно их частоты.)
Для каждого значения, т.е. для каждой строки корреляционной таблицы вычислим групповые средние
 (1.5)
(1.5)
где  - частоты пар (
- частоты пар ( ) и
) и 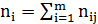 ; m – число интервалов по переменной Y.
; m – число интервалов по переменной Y.
Вычисленные групповые средние  поместим в последнем столбце корреляционной таблицы и изобразим графически в виде ломаной, называемой эмпирической линией регрессии Y по X
поместим в последнем столбце корреляционной таблицы и изобразим графически в виде ломаной, называемой эмпирической линией регрессии Y по X
Аналогично для каждого значения 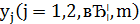 по формуле
по формуле
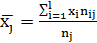 (1.6)
(1.6)
вычислим групповые средние  , где
, где 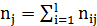 , l – число интервалов по переменной X.
, l – число интервалов по переменной X.
По виду ломанной можно определить наличие линейной корреляционной зависимости Y по X между двумя рассматриваемыми переменными, которая выражается тем точнее чем больше объем выборки n:
n= 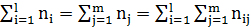 (1.7)
(1.7)
Поэтому уравнение регрессии(1.3) будем искать в виде:
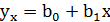 (1.8)
(1.8)
Отвлечемся на время от рассматриваемого примера и найдем формулы расчета неизвестных параметров уравнения линейной регрессии.
С этой целью применим метод наименьших квадратов, согласно которому неизвестные параметры 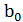 и
и 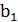 выбираются таким образом, чтобы сумма квадратов отклонений эмпирических групповых средних
выбираются таким образом, чтобы сумма квадратов отклонений эмпирических групповых средних 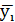 , вычисленных по формуле (1.5), от значений
, вычисленных по формуле (1.5), от значений 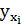 , найденных по уравнению регрессии (1.8), была минимальной:
, найденных по уравнению регрессии (1.8), была минимальной:
S= 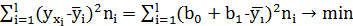 (1.9)
(1.9)
На основании необходимого условия экстремума функции двух переменных S=S( ) приравниваем к нулю ее частные производные, т.е.
) приравниваем к нулю ее частные производные, т.е.

Откуда после преобразования получим систему нормальных уравнений для определения параметров линейной регрессии:
 (1.10)
(1.10)
Учитывая (1.5) преобразуем выражение и с учетом (1.7), разделив обе части уравнений (1.10) на n, получим систему нормальных уравнений в виде:
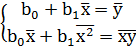 (1.11)
(1.11)
где соответствующие средние определяются по формулам:
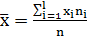 ,
, 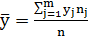 (1.12)
(1.12)
 (1.13)
(1.13)
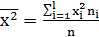 (1.14)
(1.14)
Подставляя значение 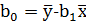 из первого уравнения системы(1.11) в уравнение регрессии (1.8), получаем
из первого уравнения системы(1.11) в уравнение регрессии (1.8), получаем
 (1.15)
(1.15)
Коэффициент b1 в уравнении регрессии, называемый выборочным коэффициентом регрессии (или просто коэффициентом регрессии) Y по Х, будем обозначать символом  . Теперь уравнение регрессии Y по Х запишется так:
. Теперь уравнение регрессии Y по Х запишется так:
 (1.15)
(1.15)
Коэффициент регрессии Yпо Х показывает, на сколько единиц в среднем изменяется переменная Y при увеличении переменной Х на одну единицу.
Решая систему (1.11), найдем
 , (1.16)
, (1.16)
где 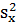 - выборочная дисперсия переменной X
- выборочная дисперсия переменной X
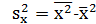 =
= 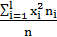 – (
– (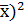 (1.17)
(1.17)
µ - выборочный корреляционный момент:
µ=  (1.18)
(1.18)
Рассуждая аналогично и полагая уравнение регрессии (1.4) линейным, можно привести его к виду:

где
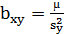 (1.21)
(1.21)
выборочный коэффициент регрессии (или просто коэффициент регрессии) Х по Y, показывающий, на сколько единиц в среднем изменяется переменная Х при увеличении переменной Y на одну единицу  =
= 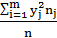 – (
– ( –выборочная дисперсия переменной Y.
–выборочная дисперсия переменной Y.
Так как числители в формулах (1.16) и (1.20) для 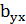 и
и  совпадают, а знаменатели – положительные величины, то коэффициент регрессии
совпадают, а знаменатели – положительные величины, то коэффициент регрессии 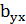 и
и  имеют одинаковые знаки, определяемые знаком
имеют одинаковые знаки, определяемые знаком 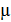 . Из уравнений регрессии (1.15) и (1.19) следует, что коэффициенты
. Из уравнений регрессии (1.15) и (1.19) следует, что коэффициенты 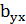 и
и  определяют угловые коэффициенты (тангенсы углов наклона) к оси Ох соответствующих линий регрессии, пересекающихся в точке (
определяют угловые коэффициенты (тангенсы углов наклона) к оси Ох соответствующих линий регрессии, пересекающихся в точке (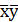 ).
).
 2020-01-14
2020-01-14 126
126








