Интерполяционные сплайны

Когда интерполяционный отрезок [a;b] велик, нет, основания считать, функцию f(x) достаточно гладкой, на [a;b], то нельзя повышать точность аппроксимации за счет увеличения степени интерполяционного многочлена.

Связано это с тем, что у многочлена n-ой степени может быть n-1 точка экстремума. При n→∞ график многочлена начинает сильно колебаться

Такое явление называют феноменом Рунге.

Поэтому более перспективным является применение кусочно-полиномиальной аппроксимации, при которой аппроксимирующая функция составляется из отдельных многочленов (сплайнов). Каждый из которых (одинаковы и наибольшей степени) определен на своем участке отрезка [a;b].

Рассмотрим аппроксимацию кусочно-линейной функции (линейный сплайн).

Пусть f(x) задана таблично на [a;b], т. е определены некоторые узлы интерполяции a≤x₀<x₁<…<x_n≤b

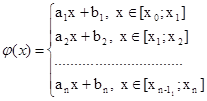   кусочно-линейная функция

Необходимо: φ(x_i)=y_i=f(x_i), для приближения функции.

Определим a_i и b_i.

x=x₀: φ(x₀)=f(x₀)=y₀                a₁x₀+b₁=y₀

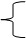x=x₁: φ(x₁)=f(x₁)=y₁                a₁x₁+b₁=y₁

                                       a₂x₁+b₂=y₁

                                                                                 x₀      x₁       x₂

Получим систему:

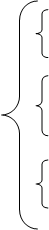
а₀x₀+b₁=y₀ (решаем по отдельности каждую систему)

a₂x₁+b₂=y₁

a₂x₁+b₂=y₁

a₂x₂+b₂=y₂                                                           (10.2)

a_nx_n-1+b_n=y_n

a_nx_n +b_n= y_n

Таким образом, получена система из 2n уравнений для поиска 2n неизвестных. Причем, система (10.2) образована из n систем линейных уравнений для 2-х неизвестных, каждая из которых может решаться независимо от остальных.

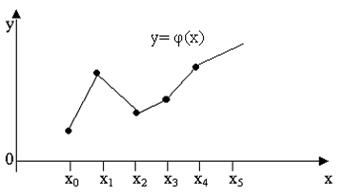
Кусочно-линейная функция φ(x) вида (10.1) внутри интервала (х_i-1;x_i), 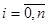непрерывна и дифференцируема, а в точках x_i,  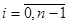непрерывна, но не дифференцируема (в этих точках к графику функции невозможно построить касательную).