Квадратичный сплайн дефекта один

Узлы этого сплайна не совпадают с узлами интерполяции функции.

Пусть узлы интерполяции заданы на [a;b]

- узлы сплайна, f(x_i)=y_i

, ,

Для сплайна n+2 узлов    

Квадратичный сплайн дефекта 1 имеет вид:

Условия:

1.)

2.) P(x) Î C'[a;b], первая непрерывная производная во всех точках [a;b]

3.) Краевые условия:

P''(a)=A; P''(b)=B;

A и B- константы и желательно разные;

Чтобы построить сплайн необходимо найти 3n+3 неизвестных коэффициента. С этой целью сформирую функцию:

P_n(x)= a_k ²+b_n +c_k

Условия:

1.) P_i+1=y_i, i=  - n+1 условий

2.) P_k = P_k+1 ,

P'_k =P'_k+1 ,

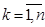
3.) P₁ =A, P''_n+1 -B – краевые условия;

Теорема 11.1. Квадр. Сплайн дефекта один, вида (11.1) для функции существует и единственен.

Теорема 11.2. Пусть функция f(x) дважды непрерывна и дифференцируема на [a;b], а P(x)- сплайн вида (11.1), тогда для , (n- связано с числом узлов интерполяции)  такие const c₀, c₁, c₂; что для  из [a;b] выполняются следующие неравенства:

| f(x)-P(x) | ≤ C₀∆²

| f '(x)-P' (x)| ≤C∆

| f ''(x)-P'' (x)| ≤C₂

где ∆- максимальное расстояние между узлами интерполяции, т.е ∆= max(x_k-x_k-1) 1≤k≤n