Выпуклые функции определяются по-разному, но наиболее естественным, пожалуй, является основанное на геометрических соображениях такое
Определение. Функция 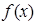 называется выпуклой вниз (вверх) на промежутке X, если любая хорда кривой
называется выпуклой вниз (вверх) на промежутке X, если любая хорда кривой 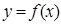 лежит не ниже (не выше) дуги, которую эта хорда стягивает.
лежит не ниже (не выше) дуги, которую эта хорда стягивает.
Далее будем рассматривать выпуклые вниз функции, а все результаты для выпуклых вверх функций при желании можно получить простым обращением знака в неравенствах.
Теорема 7 (неравенство Иенсена). Для того, чтобынепрерывнаяфункция 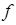 была выпуклой вниз на промежутке X, необходимо и достаточно, чтобы выполнялось неравенство
была выпуклой вниз на промежутке X, необходимо и достаточно, чтобы выполнялось неравенство 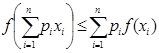 для всех
для всех 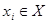 и
и 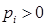 ,
, 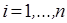 ,
, 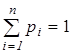 .
.
Доказательство[2]. Выясним вначале, что геометрически означает указанное неравенство при n=2. Любая точка 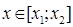 может быть представлена в виде
может быть представлена в виде 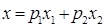 , где
, где 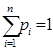 ,
, 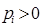 . Так как концы хорды – это точки
. Так как концы хорды – это точки 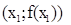 и
и 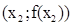 , то точка хорды с абсциссой x имеет ординату
, то точка хорды с абсциссой x имеет ординату 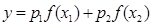 . Таким образом неравенство
. Таким образом неравенство 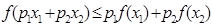 означает, что при
означает, что при 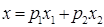 точка графика функции лежит не выше соответствующей точки хорды, и это верно для любой точки хорды, так как мы берём любые pi при условии
точка графика функции лежит не выше соответствующей точки хорды, и это верно для любой точки хорды, так как мы берём любые pi при условии 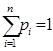 ,
, 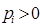 .
.
И поэтому для непрерывной функции определение выпуклости вниз и данное неравенство при n=2 эквивалентны.
Покажем сейчас, что это неравенство справедливо и для любого числа точек. Рассуждаем по индукции. Если 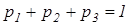 , то
, то 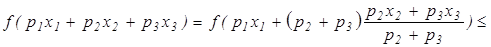
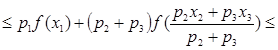
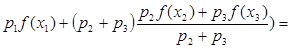
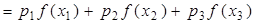 и т.д.
и т.д.
Верно и обратное, если неравенство 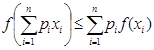 выполняется для какого-то n>2, то оно выполняется и для n=2.
выполняется для какого-то n>2, то оно выполняется и для n=2.
Действительно, перепишем 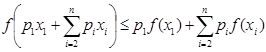 и возьмём
и возьмём 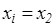 для
для 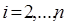 . Тогда
. Тогда 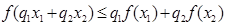 , где
, где 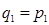 ,
, 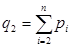 и
и 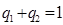 .
.
Очевидно, если все 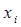 равны друг другу, то мы получаем равенство в нашем неравенстве. В противном случае равенствопри n=2
равны друг другу, то мы получаем равенство в нашем неравенстве. В противном случае равенствопри n=2 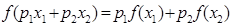 (
(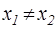 ) означает, что любая хорда кривой
) означает, что любая хорда кривой 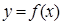 совпадает с дугой, которую эта хорда стягивает, то есть функция
совпадает с дугой, которую эта хорда стягивает, то есть функция 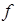 линейна. Мы можем поэтому сделать следующее
линейна. Мы можем поэтому сделать следующее
Замечание. Если функция 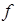 не линейна на промежутке X, то равенство в неравенстве Иенсена достигается только тогда, когда все
не линейна на промежутке X, то равенство в неравенстве Иенсена достигается только тогда, когда все 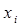 равны друг другу.
равны друг другу.
Таким образом определение выпуклой функции и данное неравенство для любого n эквивалентны. Поэтому выполнимость неравенства, если необходимо, мы можем считать аналитическим определением выпуклой функции.
Теорема 8 (аналог неравенства Иенсена). Для выпуклой вниз на отрезке 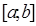 функции
функции 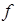 справедливо неравенство
справедливо неравенство
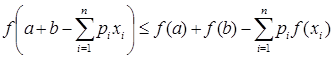 для всех
для всех 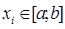 и
и 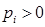 ,
, 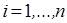 ,
, 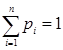 .
.
Доказательство. Представив 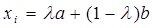 ,
, 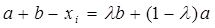 , где
, где 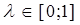 , докажем вначале вспомогательное утверждение. Справедливо неравенство
, докажем вначале вспомогательное утверждение. Справедливо неравенство 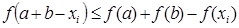 ,
, 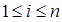 . Действительно,
. Действительно,
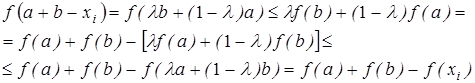
Теперь имеем:
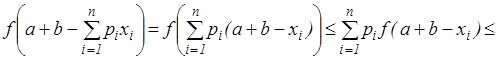
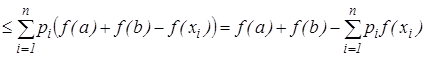 .
.
Равенство в нашем неравенстве достигается только тогда, когда обеспечивается равенство в каждой из произведённых оценок. Поэтому, если функция 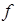 не линейна, то равенство будет только тогда, когда
не линейна, то равенство будет только тогда, когда 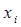 равны либо
равны либо 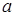 , либо
, либо 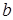 , что следует из условия
, что следует из условия 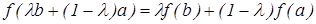 , и только тогда, когда все
, и только тогда, когда все 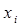 равны друг другу, что следует из условия
равны друг другу, что следует из условия 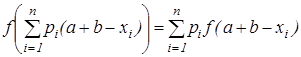 . В результате мы имеем такое
. В результате мы имеем такое
Замечание. Если функция 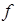 не линейна на
не линейна на 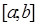 , то равенство в доказанном соотношении достигается только тогда, когда все
, то равенство в доказанном соотношении достигается только тогда, когда все 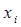 равны a или все
равны a или все 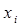 равны b.
равны b.
И важная для практического применения теорем 7 и 8, позволяющая определять выпуклость достаточно широкого класса функций
Теорема 9 (достаточный признак выпуклой функции). Если функция 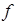 дважды дифференцируема в некотором интервале и
дважды дифференцируема в некотором интервале и 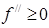 (
(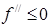 ), то
), то 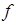 выпукла вниз (вверх) на этом интервале.
выпукла вниз (вверх) на этом интервале.
Доказательство[4]. Если 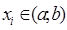 , то
, то 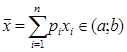 , и по формуле Тейлора
, и по формуле Тейлора 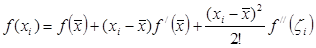 . Умножая на pi и складывая эти равенства, мы получаем
. Умножая на pi и складывая эти равенства, мы получаем 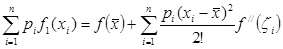 , а отсюда в силу
, а отсюда в силу 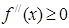 заключаем, что
заключаем, что 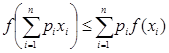 .
.
Теперь приведём определение выпуклой функции от двух переменных и сформулируем аналогичные утверждения, доказательства которых будут теми же, если не считать очевидных изменений в обозначениях.
Определение. Функция 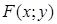 называется выпуклой вниз (вверх) в выпуклой области D (то есть области, целиком содержащей отрезок, соединяющий любые её точки), если любая хорда поверхности
называется выпуклой вниз (вверх) в выпуклой области D (то есть области, целиком содержащей отрезок, соединяющий любые её точки), если любая хорда поверхности 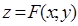 лежит не ниже (не выше) соответствующей дуги на поверхности, которую эта хорда стягивает.
лежит не ниже (не выше) соответствующей дуги на поверхности, которую эта хорда стягивает.
Теорема 10 (неравенство Иенсена). Для того, чтобынепрерывная функция 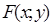 была выпуклой вниз в области D, необходимо и достаточно, чтобы выполнялось неравенство
была выпуклой вниз в области D, необходимо и достаточно, чтобы выполнялось неравенство 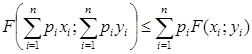 для всех
для всех 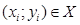 и
и 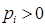 ,
, 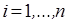 ,
, 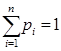 .
.
Теорема 11 (аналог неравенства Иенсена). Для выпуклой вниз в прямоугольной области 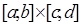 ,
, 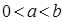 ,
, 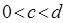 функции
функции 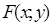 справедливо неравенство
справедливо неравенство
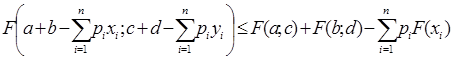 ,
,
для всех 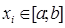 ,
, 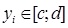 ,
, 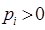 ,
, 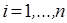 ,
, 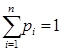 .
.
Теорема 12 (достаточный признак выпуклой функции). Если функция 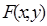 дважды дифференцируема в некоторой открытой области и
дважды дифференцируема в некоторой открытой области и 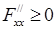 ,
, 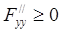 ,
, 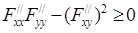
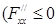 ,
, 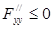 ,
, 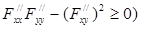 , то
, то 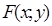 выпукла вниз (вверх) в этой области.
выпукла вниз (вверх) в этой области.
Сейчас на основе доказанных теорем перейдём непосредственно к обобщениям неравенств Коши и Гёльдера и их аналогам.
2. Обобщение неравенства Коши и его аналог
Известное неравенство Коши 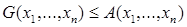 или
или 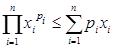 говорит о том, что среднее геометрическое и среднее арифметическое сравнимы для любых чисел xi>0 и любых весов
говорит о том, что среднее геометрическое и среднее арифметическое сравнимы для любых чисел xi>0 и любых весов 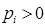 ,
, 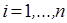 ,
, 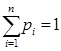 .
.
Возникает вопрос, будут ли сравнимы квази-средние, их обобщающие, то есть справедливо ли неравенство 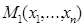 ≤
≤ 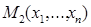 , или
, или 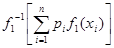 ≤
≤ 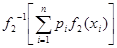 .
.
Теорема 13 (о сравнении квази-средних). Для того, чтобы выполнялось неравенство 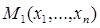 ≤
≤ 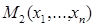 , или
, или 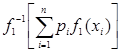 ≤
≤ 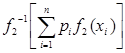 для всех
для всех 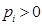 ,
, 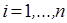 ,
, 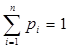 , необходимо и достаточно, чтобы функция
, необходимо и достаточно, чтобы функция 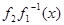 была выпуклой вниз, если
была выпуклой вниз, если 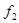 возрастает, или выпуклой вверх, если
возрастает, или выпуклой вверх, если 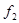 убывает.
убывает.
Доказательство[2]. Пусть 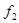 возрастает. Тогда из неравенства
возрастает. Тогда из неравенства 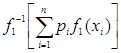 ≤
≤ 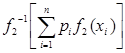 следует
следует 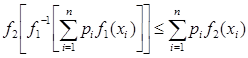 . Обозначая
. Обозначая 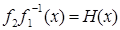 и
и 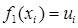 , получаем
, получаем 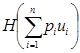 ≤
≤ 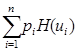 , то есть мы просто переписываем неравенство
, то есть мы просто переписываем неравенство 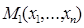 ≤
≤ 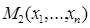 в другой форме. Новое же неравенство по теореме 7 справедливо тогда и только тогда, когда функция
в другой форме. Новое же неравенство по теореме 7 справедливо тогда и только тогда, когда функция 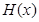 , или
, или 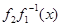 выпукла вниз.
выпукла вниз.
При убывании 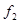 рассуждаем аналогично.
рассуждаем аналогично.
Замечание. Если 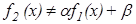 , где
, где 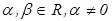 , на некотором промежутке, содержащем все
, на некотором промежутке, содержащем все 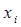 , то равенство в доказанном соотношении достигается только тогда, когда все
, то равенство в доказанном соотношении достигается только тогда, когда все 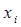 равны друг другу.
равны друг другу.
Действительно, пусть 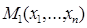 =
= 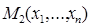 . Тогда
. Тогда 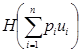 =
= 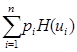 , и поэтому если функция
, и поэтому если функция 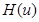 не линейна, то есть
не линейна, то есть 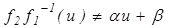 , или
, или 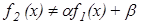 , то равенство достигается только тогда, когда все все
, то равенство достигается только тогда, когда все все 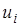 , а следовательно, и
, а следовательно, и 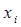 , равны друг другу.
, равны друг другу.
Отметим, что данное замечание даёт другое доказательство теоремы 4 о тождественных квази-средних.
Теорема 14. Для того, чтобы выполнялось неравенство 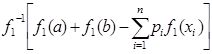 ≤
≤ 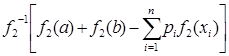 для всех
для всех 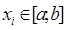 и
и 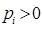 ,
, 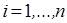 ,
, 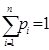 , достаточно, чтобы функция
, достаточно, чтобы функция 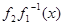 была выпуклой вниз, если
была выпуклой вниз, если 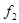 возрастает, или выпуклой вверх, если
возрастает, или выпуклой вверх, если 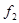 убывает.
убывает.
Доказательство. Точно так же, как и в предыдущей теореме, приводим данное неравенство к неравенству 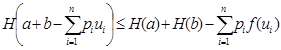 (или ему обратному при убывании
(или ему обратному при убывании 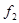 ), которое по теореме 8 вновь верно при условии, что функция
), которое по теореме 8 вновь верно при условии, что функция 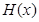 , или
, или 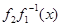 выпукла вниз (вверх()овь верно при тех же условиях________________________________________________________________________________________________).
выпукла вниз (вверх()овь верно при тех же условиях________________________________________________________________________________________________).
Замечание. Если 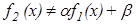 , где
, где 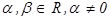 , на отрезке
, на отрезке 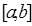 , то равенство в доказанном соотношении достигается только тогда, когда все
, то равенство в доказанном соотношении достигается только тогда, когда все 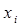 равны a или все
равны a или все 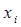 равны b.
равны b.
Теорема 13 позволяет нам как частные случаи получить известные неравенства для средних степенных [3]. Приведём эти неравенства.
Пример 1 (неравенство, характеризующее свойство монотонности среднего степенного). Для 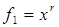 ,
, 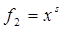 , 0< r<s функция
, 0< r<s функция 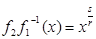 выпукла вниз (так как её вторая производная неотрицательна), и поэтому
выпукла вниз (так как её вторая производная неотрицательна), и поэтому 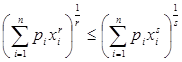 , где
, где 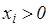 ,
, 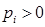 ,
, 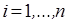 ,
, 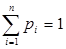 , или
, или 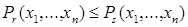 .
.
Пример 2 (неравенство Коши). Для 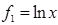 и
и 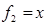 функция
функция 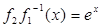 выпукла вниз, и поэтому
выпукла вниз, и поэтому 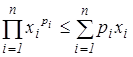 , где
, где 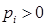 ,
, 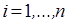 ,
, 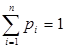 , или
, или 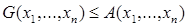 .
.
Пример 3 (неравенство Гюйгенса). Для 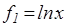 и
и 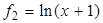 функция
функция 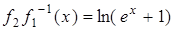 выпукла вниз, и поэтому
выпукла вниз, и поэтому 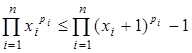 , где
, где 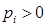 ,
, 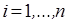 ,
, 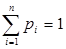 , или
, или 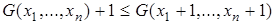 .
.
Пример 4 (неравенство Бернулли). Для 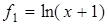 и
и 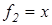 функция
функция 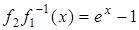 выпукла вниз, и поэтому
выпукла вниз, и поэтому 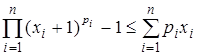 , где
, где 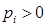 ,
, 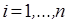 ,
, 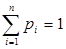 , или
, или 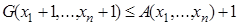 . В частности, если положить
. В частности, если положить 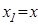 ,
, 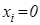 ,
, 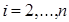 , то получим так называемое обобщённое неравенство Бернулли
, то получим так называемое обобщённое неравенство Бернулли 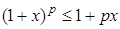 (
(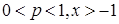 ).
).
Замечание. Равенство в вышеуказанных примерах имеет место тогда и только тогда, когда все 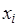 равны друг другу (так как в каждом случае
равны друг другу (так как в каждом случае 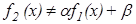 ).
).
На основании же теоремы 14 мы получаем аналоги приведённых неравенств.
Пример 1/. 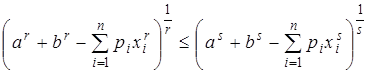 , где
, где 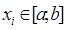 ,
, 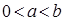 ,
, 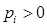 ,
, 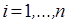 ,
, 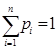 .
.
Пример 2/. 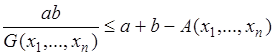 , где
, где 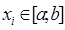 ,
, 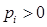 ,
, 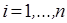 ,
, 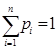 .
.
Пример 3/. 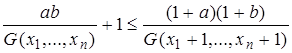 , где
, где  ,
, 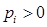 ,
, 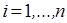 ,
, 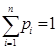 .
.
Пример 4/. 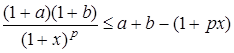 , где
, где 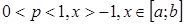 .
.
Замечание. Равенство в вышеуказанных примерах имеет место тогда и только тогда, когда все 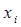 равны a или все
равны a или все 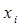 равны b.
равны b.
 2020-01-14
2020-01-14 156
156