2020-01-14
154
Один из вариантов неравенства Гёльдера (для средних значений) выглядит так [2]: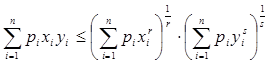 
, где 
, 
, 
, 
, 
, 
.
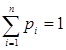Запишем его в следующей форме 
с квази-средними, заданными функциями 
, 
, 
, или 
. Снова, как и для обобщения неравенства Коши, зададимся вопросом, будет ли неравенство Гёльдера выполнятся для произвольных квази-средних.
Теорема 15. Для того чтобы выполнялось неравенство 
для всех 
, , 
, необходимо и достаточно, чтобы 
= 
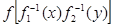была выпуклой вверх функцией, если 
возрастает, или выпуклой вниз функцией, если 
убывает.
Доказательство. Пусть возрастает. Тогда наше неравенство эквивалентно неравенству 
. Полагая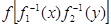 
= 
и 
, 
, переписываем 
. А новое неравенство по теореме 10 справедливо тогда и только тогда, когда функция 
или 
выпукла вверх.
При убывании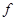 
рассуждаем аналогично.
Теорема 16. Для того, чтобы для всех 
, 
, 
, 
и 
, 
, 
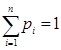выполнялось неравенство 
достаточно, чтобы функция 
= 
была выпуклой вверх, если возрастает, или выпуклой вниз, если убывает.
Доказательство точно так же, как и предыдущей теореме, сводим к теореме 11.
|
|
|
Теоремы 15 и 16 содержат как частные случаи следующие известные неравенства и их аналоги.
Пример 1 (неравенство Гёльдера). Для 
, 
, 
функция 
= 
= 
по теореме 12 выпукла вверх, если 
и 
, и поэтому 
для 
.
Пример 2 (неравенство Коши-Буняковского). Для 
, где , 
, 
.
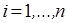Пример 1/ (аналог неравенства Гёльдера). 
, где 
, 
, 
, 
, 
, 
, 
, , 
.
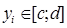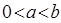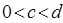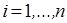Пример 2/ (аналог неравенства Коши-Буняковского). 
, где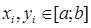 
, 
, 
.
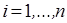Заключение
Теперь когда мы завершили изложение нашего вопроса, скажем несколько слов о возможных направлениях развития темы.
Всё доказанное о квази-средних можно разделить на две части: теоретическую (аксиоматическое задание, выделение классов новых величин) и практическую (неравенства для квази-средних как метод доказательства менее общих неравенств).
Первую часть считаем завершённой. Вторая часть остаётся открытой. Как мы видели, доказательство новых неравенств для выпуклых функций даёт возможность сформулировать новые неравенства и для квази-средних. Последние в свою очередь можно конкретизировать для их частных случаев. Так с помощью аналога неравенства Иенсена мы вывели неравенство для квази-средних, из которого в качестве следствия получили аналог неравенства Коши.
