2020-01-14
97
Найдем угловое ускорение: Угловое ускорение 
определяют из дифференциального уравнения движения:
(2.1)
где производная 
вычисляется по правилу графического дифференцирования.
Для положения 13:
где 
– угол наклона касательной к графику 
.
(2.2)
где 
– угол наклона касательной к графику 
.
Расхождение угловых ускорений составляет:
Для расчетов принимаем среднее значение:
Используем графический метод построения планов скоростей и ускорений. Определяем скорость точки В:
(2.3)
Принимаем масштабный коэффициент 
. Тогда отрезок, изображающий 
, равен:
.
Определяем скорость точки С:
,
где 
; 
.
Определяем ускорение точки В:
(2.4)
где 
– нормальная составляющая ускорения точки В, направленная от В к А; 
– тангенциальная составляющая ускорения точки В; 
сонаправлена с 
.
(2.5)
(2.6)
Принимаем масштабный коэффициент 
и находим отрезки, изображающие и :
;
.
Определяем ускорение точки С:
|
|
|
,
где 
– направлена от точки С к точке В; 
.
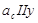(2.7)
(2.8)
По свойству подобия находим точку S2:
.
Из плана ускорений находим:
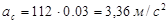
(2.9)
Определение инерционной нагрузки
Определяем силы и моменты сил инерции:
(2.10)
; (2.11)
. (2.12)
(2.13)
Силы инерции направлены противоположено ускорениям центров масс, а моменты сил инерции – противоположено угловым ускорениям звеньев.
Силовой расчет
Отделяем от механизма статически определимую структурную группу (2,3). В точке С приложена реакция 
со стороны звена 0, а в точке В – реакция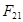 
со стороны звена 1. 
раскладываем на 
и 
. 
находим из уравнения:
(2.15)
, , находим путем построения плана сил согласно уравнению равновесия группы:
(2.14)
Принимаем масштабный коэффициент 
и находим отрезки, изображающие известные силы:
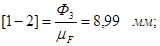
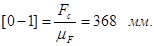
Из плана сил находим:
Рассматриваем кривошип 1. В точке В приложена известная реакция со стороны звена 2: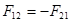 
, а в точке А – реакция 
, которую находим путем построения плана сил согласно уравнению равновесия:
(2.15)
Оценка точности расчетов
Находим относительную погрешность 
Синтез зубчатого зацепления
