2020-01-14
96
Исходные данные для открытой зубчатой передачи:
– числа зубьев колёс;
–модуль зубчатых колес;
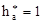– коэффициент высоты головки зуба;
– коэффициент радиального зазора;
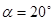– угол профиля исходного контура.
Минимальное число зубьев:
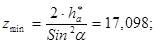
Коэффициентов смещения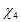 
и 
исходного контура.
Коэффициенты смещения 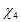и должны соответствовать условию: (При отсутствии подрезания зубьев.)
;
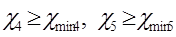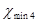и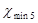 
определяем по формуле:
; 
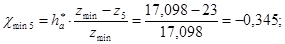
Выбираем из таблиц коэффициенты смещения 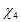и :
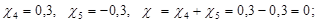
Угол зацепления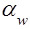 
:
По таблице эвольвентных функций находим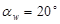 
.
Радиусы делительных окружностей:
Радиусы основных окружностей:
Радиусы начальных окружностей:
Коэффициенты воспринимаемого смещения:
Коэффициент уравнительного смещения:
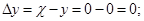
Межосевое расстояние передачи.
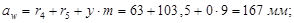
Радиусы окружностей впадин.
Радиусы окружностей вершин:
Высота зубьев колес:
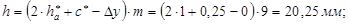
Окружной делительный шаг:
Угловой шаг.
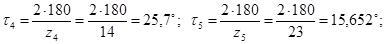
Толщины зубьев по окружности вершин:
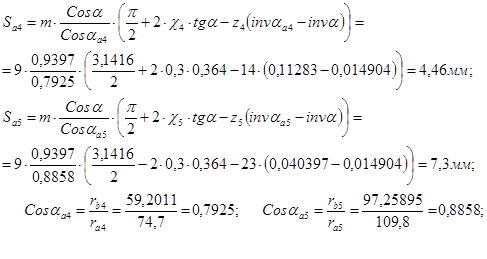
Толщины зубьев по дуге делительной окружности:
Толщины зубьев по основным окружностям:
;
.
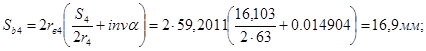Толщины зубьев по начальным окружностям:
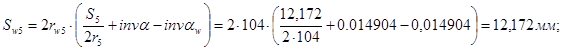
Радиусы кривизны эвольвент в нижних точках активных профилей:
;
Радиусы кривизны эвольвент в граничных точках активных профилей:
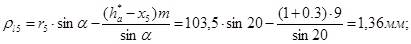
Коэффициент перекрытия:
Проверка подрезания зубьев:
;
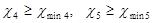
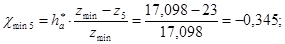
Т.к. 
и 
, подрезание отсутствует.
Проверка отсутствия интерференции зубьев:
и 
.Т.к. 
и 
, то интерференция зубьев отсутствует.
Проверка плавности работы передачи:
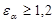. Т.к. 
, то обеспечивается достаточная плавность.
Проверка заострения зубьев:
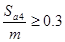и 
Т.к. 
, то заострение зубьев отсутствует.
При вычерчивании картины зацепления профилей используют длину шага между зубьями по делительным окружностям, равную 
, основного шага по линии зацепления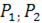 
, равную 
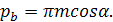точки контакта профилей расположены на линии зацепления 
.
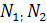В точках 
изображают пунктиром профили зубьев в момент начала и в момент окончания зацепления зубьев.
Пользуясь схемой передачи, вычерченной в масштабе длин, измеряют длины отрезков и рассчитывают коэффициенты перекрытия 
и удельного скольжения.
Чертеж зацепления построен в масштабе 
Геометрический синтез планетарного механизма
По заданному передаточному отношению 
и числу сателлитов 
требуется определить числа зубьев колес 
, исходя из условий соосности, сборки и соседства сателлитов, а также отсутствия подрезания и интерференции зубьев.
Используем формулу Виллиса:
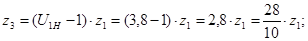
Из условия соосности колес 
имеем:
.
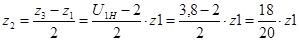Принимаем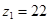 
(при других значениях 
не будет выполняться условие сборки) и находим:
; 
.
Условие сборки:
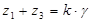, где 
– любое целое число.
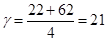– условие выполняется т.к. 
– целое число.
Условие соседства сателлитов:
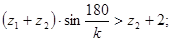
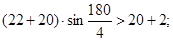
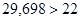– условие выполняется. Т.к. 
и 
, то подрезания и интерференции зубьев не будет (в случае колес без смещения).
Радиусы делительных окружностей:
.
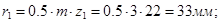
Чертеж планетарного механизма зацепления построен в масштабе 
