Функции Бесселя с произвольным значком

бессель цилиндрическая функция

Функции Бесселя, рассмотренные в пункте 1, составляют частный случай цилиндрических функций более общего вида, известных под названием функций Бесселя первого рода с произвольным значком . Чтобы определить эти функции, рассмотрим ряд

где  – комплексное переменное, принадлежащее плоскости с разрезом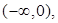

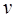 – параметр, который может принимать любые вещественные или комплексные значения.

Легко видеть, что данный ряд сходится при любых 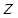 и , причем в области ,  (  – произвольно большие фиксированные числа) сходимость равномерна по отношению к каждому из переменных.

Действительно, начиная с достаточного большого , отношение модулей последующего члена ряда к предыдущему, равное величине

не будет превосходить некоторой правильной положительной дроби , не зависящей от  и . Отсюда, согласно известному признаку сходимости, следует, что рассматриваемый ряд сходится равномерно в указанной области [4].

Так как члены ряда представляют собой регулярные функции в плоскости с разрезом  сумма ряда определяет некоторую функцию комплексного переменного , регулярную в рассматриваемой разрезанной плоскости. Эта функция называется функцией Бесселя первого рода с индексом 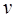 и обозначается символом . Таким образом,

 

                      (2.1)

 

Нетрудно показать, что определенная таким образом функция есть частное решение уравнения

 

                                                                (2.2)

 

Действительно, обозначая левую часть этого уравнения  и полагая 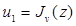, мы находим, так же как в пункте 1,

где  – коэффициенты ряда (2.1),

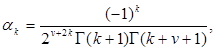
откуда следует, что

Так как при фиксированном , принадлежащем плоскости с разрезом  члены ряда (2.1) представляют собой целые функции переменного , то из равномерной сходимости по отношению к этому переменному вытекает, что функция Бесселя первого рода, рассматриваемая как функция своего значка, есть целая функция . При целом  и ряд (2.1) переходит в ряд (1.2), поэтому функции, определенные в настоящем параграфе, являются обобщением функций Бесселя с целым положительным значком, изученных в пункте 2. При  равном целому отрицательному числу , первые  членов ряда (2.1) обращаются в нуль, и рассматриваемая формула может быть записана в виде

откуда следует

 

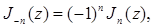
                                                    (2.3)

Таким образом, функции Бесселя с отрицательным целым значком отличаются от соответствующих функций с положительным значком только постоянным множителем.

Полученное соотношение вместе с формулами (1.10 – 1.11) показывает, что разложение (1.12) может быть записано в виде

 

                                         (2.4)

 

Многие равенства, установленные ранее для функций Бесселя с целым положительным значком, переносятся на функции с произвольным индексом без каких-либо изменений. Так, например, имеют место соотношения:

 

                      (2.5)

 

                          (2.6)

 

    (2.7)

 

представляющие собой обобщение соответствующих формул пункта 2. Доказательство формул (2.5 – 2.6) повторяет рассуждения этого параграфа и поэтому не приводится. Формулы (2.7) получаются путем повторного применения равенств (2.6).