С функциями Бесселя тесно связаны две часто встречающиеся в приложениях функции  и
и 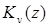 , которые для
, которые для  , принадлежащего плоскости с разрезом вдоль отрицательной полуоси
, принадлежащего плоскости с разрезом вдоль отрицательной полуоси 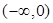 и произвольного
и произвольного  , могут быть определены при помощи формул:
, могут быть определены при помощи формул:
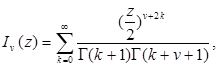
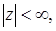
 (6.1)
(6.1)
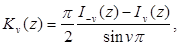

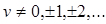 (6.2)
(6.2)
и при целом 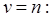
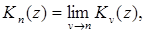
 (6.3)
(6.3)
Повторяя рассуждения пункта 2, получаем, что  и
и 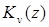 представляют собой регулярные функции
представляют собой регулярные функции  в плоскости с разрезом
в плоскости с разрезом 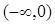 и целые функции
и целые функции  .
.
Рассматриваемые функции просто связаны с функциями Бесселя от аргумента 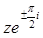 .
.
Действительно, предположим, что 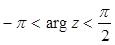 . Тогда
. Тогда 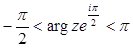 и из (2.1) следует
и из (2.1) следует
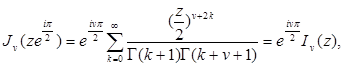
откуда
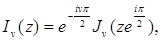 (6.4)
(6.4)
для всех 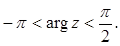
Аналогично из формулы (5.4) получаем для таких же 
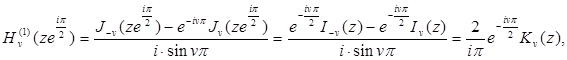
откуда
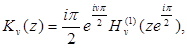
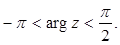 (6.5)
(6.5)
Для значений 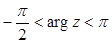 функции
функции  и
и  могут быть выражены через функции Бесселя от аргумента
могут быть выражены через функции Бесселя от аргумента 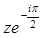 . Мы имеем
. Мы имеем

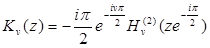 (6.6)
(6.6)
для всех  .
.
На основании полученных соотношений функции  и
и 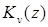 называются функциями Бесселя мнимого аргумента. Функция
называются функциями Бесселя мнимого аргумента. Функция 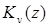 известна в литературе также под названием функции Макдональда.
известна в литературе также под названием функции Макдональда.
Из выведенных формул непосредственно следует, что рассматриваемые функции представляют собой линейно независимые решения дифференциального уравнения
 (6.7)
(6.7)
которое отличается от уравнения Бесселя только знаком одного члена и переходит в него при подстановке  .
.
Уравнение (6.7) часто встречается в математической физике. Общий интеграл этого уравнения при произвольном 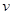 может быть записан в виде
может быть записан в виде
 (6.8)
(6.8)
Функции  и
и  удовлетворяют простым рекуррентным соотношениям:
удовлетворяют простым рекуррентным соотношениям:
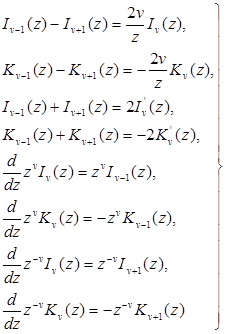 (6.9)
(6.9)
и т.д.
Рекуррентные формулы, содержащие функции 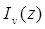 , доказываются подстановкой в них ряда (6.1). Соответствующие формулы для функций
, доказываются подстановкой в них ряда (6.1). Соответствующие формулы для функций 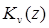 при
при 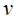 , отличном от целого числа, проверяются путем подстановки в них выражения (6.2) и использования формул первой группы. Справедливость последних соотношений при целом
, отличном от целого числа, проверяются путем подстановки в них выражения (6.2) и использования формул первой группы. Справедливость последних соотношений при целом 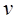 следует из непрерывности рассматриваемых функций по отношению к значку.
следует из непрерывности рассматриваемых функций по отношению к значку.
Укажем еще две полезные формулы:
 (6.10)
(6.10)
первая из которых вытекает из (6.1), если принять во внимание, что при  первые
первые 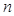 членов разложения обращаются в нуль, в то время как вторая является прямым следствием определения функции Макдональда (6.2).
членов разложения обращаются в нуль, в то время как вторая является прямым следствием определения функции Макдональда (6.2).
Разложение функции  при
при 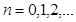 может быть получено из (6.3) методом пункта 5. Приведем окончательный результат вычисления:
может быть получено из (6.3) методом пункта 5. Приведем окончательный результат вычисления:
 (6.11)
(6.11)

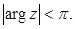
Здесь  – логарифмическая производная гамма-функции, значения которой могут быть найдены по формулам (4.2). Для случая
– логарифмическая производная гамма-функции, значения которой могут быть найдены по формулам (4.2). Для случая 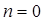 первую из сумм надлежит считать равной нулю.
первую из сумм надлежит считать равной нулю.
Из (6.11) вытекает, что асимптотическое поведение функции 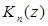 при
при  определяется формулами
определяется формулами

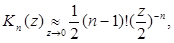
 (6.12)
(6.12)
поэтому 
 2020-01-14
2020-01-14 471
471








