Разложение в ряд функции Бесселя второго рода с целым значком

 

Для того чтобы получить разложение в ряд функции , достаточно воспользоваться формулой (3.7) и вычислить производные по значку , исходя из разложения (2.1), причем, ввиду соотношения (3.10), можно ограничиться рассмотрением случая целых положительных

Так как ряд (2.1), по доказанному, сходится равномерно по отношению к , мы можем дифференцировать его почленно и получим тогда [2]

где  – логарифмическая производная гамма-функции.

Аналогично имеем

При  и  поэтому первые  членов ряда принимают неопределенный вид. Воспользовавшись известными формулами теории гамма-функции

;

получим для таких

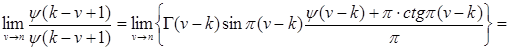
поэтому

где введен новый значок суммирования

Из формулы (3.7) следует, что искомое разложение функции Бесселя второго рода с целым положительным значком имеет вид

 

                                                                   (4.1)

 

где в случае 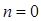 первую сумму надлежит положить равной нулю.

Значения логарифмической производной гамма-функции могут быть вычислены по формулам:

 

                                                         (4.2)

 

где  – постоянная Эйлера,

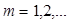
Принимая во внимание равенство (1.2), мы можем представить разложение (4.1) в несколько другом виде, именно:

 

                                 (4.3)

 

Из (4.1) вытекает, что при  справедливы асимптотические формулы

                           (4.4)

 

показывающие, что  когда