Функции Бесселя третьего рода

К цилиндрическим функциям относятся также функции Бесселя третьего рода или функции Ханкеля  и , которые для произвольного  и , принадлежащего плоскости с разрезом вдоль полуоси , определяются при помощи формул

                       (5.1)

где  – функции Бесселя первого и второго рода.

Целесообразность введения этих функций обусловлена тем, что рассматриваемые линейные комбинации из  и  обладают наиболее простыми асимптотическими разложениями при больших  (пункт 8) и часто встречаются в приложениях.

Из определения функций Ханкеля следует, что эти функции представляют собой регулярные функции  в плоскости с разрезом 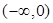 и целые функции . Очевидно, что рассматриваемые функции линейно независимы между собой и по отношению к , так что общий интеграл уравнения Бесселя (3.1) может быть, наряду с (3.8), представлен в одной из следующих форм:

(5.2)

где  – произвольные постоянные.

Являясь линейными комбинациями функций  и , функции Ханкеля удовлетворяют тем же рекуррентным соотношениям, что и эти функции, например,

                                                    (5.3)

и т.д.

Если с помощью (3.5) исключить из (5.1) функцию Бесселя второго рода, то получим

                                                          (5.4)

откуда вытекают важные соотношения:

                                                           (5.5)