2020-01-14
175
Цилиндрические функции обладают простыми асимптотическими представлениями, удобными для аппроксимации этих функций при больших по модулю значениях 
и фиксированном значении индекса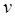 
[5]. Главные члены этих формул можно получить, исходя из дифференциальных уравнений, которым удовлетворяют рассматриваемые функции.
Из цилиндрических функций наиболее простые асимптотические представления имеют функции третьего рода.
Чтобы получить асимптотическое представление функции 
, воспользуемся равенством
(8.1)
и преобразуем его с помощью подстановки 
. Тогда получим
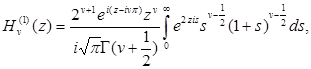(8.2)
Заменяя множитель 
биноминальным разложением с остаточным членом
и интегрируя почленно, находим
(8.3)
где 
Предположим, что 
(
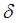– произвольное малое положительное число) и будем временно считать, что 
выбрано так, что 
Оценка остаточного члена по модулю тогда дает
при фиксированном 
Таким образом, для больших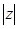 
|
|
|
(8.4)
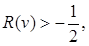
Покажем, что условие, наложенное на 
, может быть отброшено. Действительно, если 
, то можно выбрать такое 
, что 
. Представив 
с помощью формулы (8.4), где 
заменено на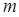 
, и замечая, что
мы снова приходим к прежнему результату.
Также легко с помощью соотношения 
освободиться от ограничения, наложенного на параметр 
.
Наконец, если воспользоваться вместо (8.1) интегральным представлением несколько более общего вида, можно показать, что найденная асимптотическая формула остается справедливой в более широком секторе 
[5].
Таким образом, окончательно для больших 
(8.5)
где 
Асимптотическое представление для функции 
получается аналогичным способом из формулы
(8.6)
и имеет следующий вид:
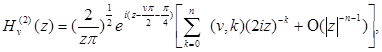
(8.7)
Асимптотические представления для цилиндрических функций первого и второго рода следуют из выведенных формул (8.5) и (8.7) и соотношений (5.1). Мы находим
(8.8)
(8.9)
Асимптотические формулы для модифицированных цилиндрических функций могут быть получены с помощью соотношений пункта 6.
Окончательные формулы имеют следующий вид:
(8.10)
(8.11)
знак 
соответствует 
При условии, что 
, второе слагаемое в (8.10) будет мало, и эта формула может быть записана в виде
(8.12)
Из (8.5) и (8.7 – 8.12) следует, что расходящиеся ряды, получающиеся, если формально положить 
, являются асимптотическими для функций, стоящих в левых частях рассматриваемых равенств.
|
|
|
Способ, при помощи которого выведены рассматриваемые формулы, дает только порядок величины остаточного члена, но не позволяет сделать более точных заключений. При специальных предположениях относительно 
и 
можно, путем некоторого видоизменения рассуждений, получить значительно более точные результаты. Так, например, можно показать, что если и 
– вещественные положительные числа и число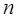 
взято настолько большим, что 
то остатки асимптотических разложений для 
и 
будут численно меньше первых отбрасываемых членов. В асимптотическом представлении для 
тот же результат имеет место при 
.
