Основными задачами кинематического исследования механизмов являются:
· определение положений звеньев
· определение скоростей и ускорений точек;
· определение угловых скоростей и ускорений звеньев.
Ведущее звено - кривошип и считаем его угловую скорость  , рад/с постоянной. Исследования проводим графоаналитическими методами. Так, положения звеньев определяем методом засечек при построении плана механизма, скорости и ускорения различных точек механизма находим с помощью построения планов скоростей и ускорений.
, рад/с постоянной. Исследования проводим графоаналитическими методами. Так, положения звеньев определяем методом засечек при построении плана механизма, скорости и ускорения различных точек механизма находим с помощью построения планов скоростей и ускорений.
Построение планов механизма
Кинематическую схему строим методом засечек.
Выбираем масштаб построения с таким расчетом, чтобы планы положений механизма заняли примерно 1/5…1/4 часть площади формата А1 или полную площадь формата А4.
Выбираем точку О1. Проводим окружность радиуса  . Длину отрезка, изображающего звено О1А выбираем произвольно из соображения размещения схемы механизма на листе выбранного формата.
. Длину отрезка, изображающего звено О1А выбираем произвольно из соображения размещения схемы механизма на листе выбранного формата.
O1A = 230 мм – заданная длина кривошипа.
 = 46 мм - длина кривошипа на чертеже.
= 46 мм - длина кривошипа на чертеже.
Вычисляем масштаб построения  ;
;
 = 0,23 / 46 = 0,005 м/мм
= 0,23 / 46 = 0,005 м/мм
В соответствии с выбранным масштабом определяем длины всех линейных величин.
Вычисляем длину отрезка АВ:  = 0,575 / 0,005 = 115 мм.
= 0,575 / 0,005 = 115 мм.
Вычисляем длину отрезка О2В:  = 0,92 / 0,005 = 184 мм.
= 0,92 / 0,005 = 184 мм.
Вычисляем длину отрезка АD:  = 0,16 / 0,005 = 32 мм.
= 0,16 / 0,005 = 32 мм.
Строим план механизма в заданном положении (φ = 2250.) Заданное положение механизма, вычерчиваем основными линиями. (Остальные положения механизма вычерчиваем тонкими сплошными линиями). Вычерчиваем начальное звено О1А в заданном положении. Из точки A делаем засечку радиусом  . Из точки О2 делаем засечку радиусом
. Из точки О2 делаем засечку радиусом  . Находим место пересечения засечек – получаем положение точки B. Находим положение точки D.
. Находим место пересечения засечек – получаем положение точки B. Находим положение точки D.
Разбиваем окружность на восемь равных частей. Строим 8 положений механизма, чтобы представить себе как он работает и какую траекторию описывает точка D. Последовательно помещаем шарнир А в равноотстоящие положения 2, 3…7, 8 в направлении вращения кривошипа, методом засечек определяем соответствующие положения точек B и D кривошипа.
Для получения траектории точки D необходимо последовательно соединить плавной кривой все восемь положений точки D с помощью лекал. Находим крайние положения механизма (M1N1ТВ1 и M2N2ТВ2).
Построение планов скоростей механизма
Кривошип (1) вращается в направлении, указанном стрелкой с постоянной угловой скоростью  .
.
Угловая скорость вращения кривошипа
 =
=  = 25,1 рад/с
= 25,1 рад/с
На чертеже выбираем точку – полюс плана скоростей. Обозначим ее 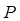 . Скорость точки О1 равна нулю, т.е. отрезок на плане скоростей будет равен нулю – точка
. Скорость точки О1 равна нулю, т.е. отрезок на плане скоростей будет равен нулю – точка 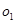 совпадет с точкой
совпадет с точкой  .
.
Вектор скорости точки А направлен перпендикулярно звену 1 в сторону направления вращения.
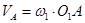 = 25,1 ∙ 0,23 = 5,8 м/с
= 25,1 ∙ 0,23 = 5,8 м/с
Вектор скорости точки S1 направлен перпендикулярно звену 1 в сторону направления вращения.
 = 25,1 ∙ 0,115 = 2,9 м/с
= 25,1 ∙ 0,115 = 2,9 м/с
Из полюса (точки  ) построим вектор
) построим вектор  , соответствующий вектору скорости
, соответствующий вектору скорости 
Вектор  начинается в точке
начинается в точке  , направлен перпендикулярно кривошипу.
, направлен перпендикулярно кривошипу.
Конец вектора обозначим точкой 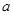 .
.
После того, как длина вектора на чертеже определена, вычисляем масштаб построения планов скоростей:
 .
.
Вектор на плане, соответствующий скорости центра тяжести первого звена  -
-  совпадет по направлению с вектором
совпадет по направлению с вектором  , его длина будет зависеть от масштаба построения:
, его длина будет зависеть от масштаба построения:
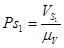 =
=  = 29 мм
= 29 мм
Переходим к анализу линейных скоростей точек структурной группы (звенья 2, 3).
Звено 2 совершает плоскопараллельное движение, звено 3 вращательное.
Для нахождения скорости точки B составляем векторное уравнение:

Точка B движется по окружности с центром в О2.
Векторное уравнение можно решить, если в нем не более двух неизвестных.
| Вектор, входящий в уравнение | 
| 
| 
|
| Направление вектора |  - перпендикулярна О2В - перпендикулярна О2В
| 
| 
|
| Модуль вектора (его численное значение) м/с | ? | вычислено | ? |
Решаем векторное уравнение графически.
В правой части уравнения складываются два вектора  :
:
1. Надо построить вектор соответствующий  - но он на плане уже есть, (отрезок
- но он на плане уже есть, (отрезок  ) – приходим в точку
) – приходим в точку 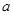 . Из точки
. Из точки 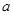 надо построить вектор, соответствующий
надо построить вектор, соответствующий  , но для этого вектора задано только направление. Проводим из точки
, но для этого вектора задано только направление. Проводим из точки 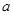 прямую
прямую  .
.
2. Переходим к левой части уравнения – в ней указан только вектор  . Т.е. выходя из полюса надо построить вектор, соответствующий
. Т.е. выходя из полюса надо построить вектор, соответствующий  . Но для него известно только направление – из точки
. Но для него известно только направление – из точки  проводим прямую перпендикулярную О2В.
проводим прямую перпендикулярную О2В.
Точка пересечения прямых – точка 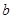 . Расставляем стрелки, определяющие направление векторов. Направление в правой части уравнения задано вектором
. Расставляем стрелки, определяющие направление векторов. Направление в правой части уравнения задано вектором  . Направление вектора в левой части уравнения – из полюса. Вектор
. Направление вектора в левой части уравнения – из полюса. Вектор  на плане скоростей соответствует скорости
на плане скоростей соответствует скорости  .
.
Замеряем длины получившихся векторов ab,  и, учитывая масштаб, вычисляем скорости:
и, учитывая масштаб, вычисляем скорости:
 = 0,1 · 37,4 = 3,74 м/с;
= 0,1 · 37,4 = 3,74 м/с;
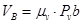 = 0,1 · 51,6 = 5,16 м/с.
= 0,1 · 51,6 = 5,16 м/с.
 ;
;
Угловая скорость шатуна 
Для определения направления  мысленно переносим вектор
мысленно переносим вектор  (вектор
(вектор  на плане скоростей) в точку В плана механизма и смотрим как будет вращаться звено 2 относительно точки А под действием этого вектора.
на плане скоростей) в точку В плана механизма и смотрим как будет вращаться звено 2 относительно точки А под действием этого вектора.
Определяем скорость точки D.


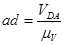 =
= 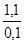 = 11 мм
= 11 мм
Вектор, соответствующий 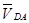 направлен
направлен  .
.
Проведя построения на плане скоростей, находим вектор, соответствующий  .
.
 = 0,1 · 48,7 = 4,87 м/с.
= 0,1 · 48,7 = 4,87 м/с.
Аналогично находим скорость точки S2.

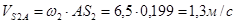
АS2 = 39,8 ∙ 0,005 = 0,199 м
 =
=  = 13 мм
= 13 мм
Вектор, соответствующий  направлен
направлен  .
.
Проведя построения на плане скоростей, находим вектор, соответствующий 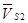 .
.
 = 0,1 · 49,6 = 4,96 м/с.
= 0,1 · 49,6 = 4,96 м/с.
Коромысло 3 вращается относительно точки О2. Угловая скорость коромысла

Для определения направления  мысленно переносим вектор
мысленно переносим вектор  (вектор
(вектор  на плане скоростей) в точку В плана механизма и смотрим, как будет вращаться звено 3 под действием этого вектора.
на плане скоростей) в точку В плана механизма и смотрим, как будет вращаться звено 3 под действием этого вектора.
Вектор скорости точки S3 направлен перпендикулярно звену 3 в сторону направления вращения.
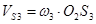 = 5,6 ∙ 0,46 = 2,6 м/с
= 5,6 ∙ 0,46 = 2,6 м/с
 =
=  = 26 мм
= 26 мм
Построение планов ускорений механизма
Кривошип вращается в направлении, указанном стрелкой с постоянной угловой скоростью  .
.
В общем случае ускорение точки вращающегося тела складывается из векторов ускорения нормального и ускорения тангенциального.
Вектор нормального ускорения точки направлен из точки к центру вращения и зависит от угловой скорости звена и расстояния точки от центра вращения. Вектор тангенциального ускорения точки направлен по касательной к траектории её движения (т.е.перпендикулярен ускорению нормальному) и зависит от углового ускорения вращения и расстояния точки от центра вращения.
Угловая скорость кривошипа постоянна, угловое ускорение равно нулю  , тангенциальная составляющая ускорения точки А равна нулю
, тангенциальная составляющая ускорения точки А равна нулю  .
.
Ускорение точки А равно нормальному ускорению и направлено вдоль звена 1 к центру вращения
 = 25,12 ∙ 0,23 = 145 м/с2
= 25,12 ∙ 0,23 = 145 м/с2
Ускорение точки  равно нормальному ускорению этой точки и направлено вдоль звена 1 к центру вращения
равно нормальному ускорению этой точки и направлено вдоль звена 1 к центру вращения
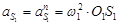 = 25,12 ∙ 0,115 = 72,5 м/с2
= 25,12 ∙ 0,115 = 72,5 м/с2
На чертеже выбираем точку – полюс. Обозначим ее  . Ускорение точки О1 равно нулю, т.е. отрезок на плане скоростей будет равен нулю – точка О1 совпадет с точкой
. Ускорение точки О1 равно нулю, т.е. отрезок на плане скоростей будет равен нулю – точка О1 совпадет с точкой 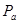 .
.
Откладываем из полюса параллельно звену О1А вектор  , соответствующий ускорению
, соответствующий ускорению  .
.
Вычисляем масштаб построения 

Построим на плане вектор 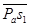 . Его длина на чертеже:
. Его длина на чертеже:
 . Направление совпадает с
. Направление совпадает с  .
.
Шатун (звено 2) совершает плоско-параллельное движение (ускорение точек такого звена складывается из ускорения полюса и ускорений, возникающих при повороте звена относительно полюса)
Если рассматривать точку В как принадлежащую звену 2, то можно записать: 
Коромысло (звено 3) совершает вращательное движение относительно точки О2.
Если рассматривать точку В как принадлежащую звену 3,то: 
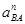 - вектор нормальной составляющей ускорения в движении точки В относительно А, направленный по ВА от точки В к точке А:
- вектор нормальной составляющей ускорения в движении точки В относительно А, направленный по ВА от точки В к точке А:
 = 6,52 ∙ 0,575 = 24,3 м/с2
= 6,52 ∙ 0,575 = 24,3 м/с2
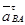 - вектор тангенциальной составляющей ускорения в движении точки В относительно точки А, направление которого перпендикулярно к нормальной составляющей ускорения, т.е. перпендикулярно к АВ.
- вектор тангенциальной составляющей ускорения в движении точки В относительно точки А, направление которого перпендикулярно к нормальной составляющей ускорения, т.е. перпендикулярно к АВ.
 - вектор нормальной составляющей ускорения в движении точки В относительно неподвижной точки 02, направленный вдоль В02 от точки В к точке О2
- вектор нормальной составляющей ускорения в движении точки В относительно неподвижной точки 02, направленный вдоль В02 от точки В к точке О2
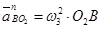 = 5,62 ∙ 0,92 = 28,9 м/с2
= 5,62 ∙ 0,92 = 28,9 м/с2
 - вектор тангенциальной составляющей ускорения в движении точки В относительно точки O2, направление которого перпендикулярно к нормальной составляющей
- вектор тангенциальной составляющей ускорения в движении точки В относительно точки O2, направление которого перпендикулярно к нормальной составляющей  , т.е. перпендикулярно к O2B).
, т.е. перпендикулярно к O2B).

| Вектор, входящий в уравнение | 
| 
| 
| 
| 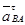
|
| Направление вектора |  ;
от В к О2 ;
от В к О2
| 
| на плане |  ;
от B к A ;
от B к A
| 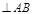
|
| Модуль вектора (его численное значение) м/с2 | вычислено | ? | вычислено | вычислено | ? |
Решаем векторное уравнение:
1) Из полюса  переходим в точку
переходим в точку  , из точки
, из точки  проводим прямую параллельно АВ и откладываем
проводим прямую параллельно АВ и откладываем  , что соответствует вектору нормального ускорения в повороте точки В относительно А, и получаем точку
, что соответствует вектору нормального ускорения в повороте точки В относительно А, и получаем точку 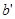 .
.

Теперь надо построить вектор соответствующий 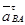 , но у него задано только направление. Из точки
, но у него задано только направление. Из точки  проводим линию
проводим линию 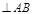 .
.
2) Из полюса откладываем  параллельно О2В в направлении от В к О2, что соответствует вектору нормального ускорения точки В относительно О2, и получаем точку
параллельно О2В в направлении от В к О2, что соответствует вектору нормального ускорения точки В относительно О2, и получаем точку 
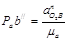

Из точки  надо построить вектор, соответствующий
надо построить вектор, соответствующий  , но у него известно только направление. Из точки
, но у него известно только направление. Из точки  проводим линию
проводим линию  .
.
3) Линии, проведенные из точек  и
и  , пересекаются в точке
, пересекаются в точке 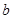 . Проводим вектор
. Проводим вектор  - вектор соответствует ускорению точки В.
- вектор соответствует ускорению точки В.
Указываем на плане направления всех векторов.
Замеряем на плане длины полученных отрезков и вычисляем ускорения:
 = 69,4 ∙ 2 = 138,8 м/с2.
= 69,4 ∙ 2 = 138,8 м/с2.
 = 70,5 ∙ 2 = 141 м/с2.
= 70,5 ∙ 2 = 141 м/с2.
 = 45,5 ∙ 2 = 91 м/с2.
= 45,5 ∙ 2 = 91 м/с2.
 = 47,7 ∙ 2 = 95,4 м/с2.
= 47,7 ∙ 2 = 95,4 м/с2.
Вычисляем угловые ускорения:
Угловое ускорение шатуна (2-е звено): 
Угловое ускорение коромысла (3-е звено): 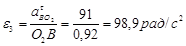
Направления угловых ускорений определяются в соответствии с направлениями 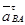 и
и  .
.
Для определения направления  мысленно переносим вектор
мысленно переносим вектор  (вектор
(вектор 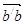 на плане ускорений) в точку В плана механизма и смотрим в какую сторону будет вращаться звено 2 относительно точки А под действием этого вектора. В нашем случае угловое ускорение
на плане ускорений) в точку В плана механизма и смотрим в какую сторону будет вращаться звено 2 относительно точки А под действием этого вектора. В нашем случае угловое ускорение  направлено по ходу часовой стрелки.
направлено по ходу часовой стрелки.
Для определения направления  мысленно переносим вектор
мысленно переносим вектор  (вектор
(вектор  на плане ускорений) в точку В плана механизма и смотрим в какую сторону будет вращаться звено 3 относительно точки О2 под действием этого вектора.
на плане ускорений) в точку В плана механизма и смотрим в какую сторону будет вращаться звено 3 относительно точки О2 под действием этого вектора.
Составляем векторное уравнение для определения ускорения 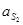

 = 6,52 ∙ 0,199 = 8,4 м/с2.
= 6,52 ∙ 0,199 = 8,4 м/с2.
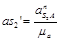

 = 241,4 ∙ 0,199 = 48 м/с2
= 241,4 ∙ 0,199 = 48 м/с2

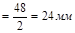
| Вектор, входящий в уравнение | 
| 
| 
| 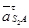
|
| Направление вектора | ? | на плане |  ;
от S2 к A ;
от S2 к A
|  в сторону определяемую направлением в сторону определяемую направлением  
|
| Модуль вектора (его численное значение) м/с2 | ? | вычислено | вычислено | вычислено |
Решаем векторное уравнение графически:
1) Из полюса  переходим в точку
переходим в точку 
2) Отложив на плане от точки a вектор 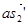 , получим точку
, получим точку  . Направление вектора
. Направление вектора  - параллельно АS2. Через полученную точку
- параллельно АS2. Через полученную точку 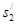 проводим линию
проводим линию  .
.
3) Из точки 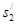 вдоль проведенной линии откладываем вектор
вдоль проведенной линии откладываем вектор 
4) из полюса  - стоим вектор
- стоим вектор 
Измеряем длину отрезка  . Вычисляем
. Вычисляем  = 61,6 ∙ 2 = 123,2 м/с2
= 61,6 ∙ 2 = 123,2 м/с2
Аналогично находим ускорение точки D.

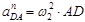 = 6,52 ∙ 0,16 = 6,8 м/с2.
= 6,52 ∙ 0,16 = 6,8 м/с2.


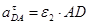 = 241,4 ∙ 0,16 = 38,6 м/с2
= 241,4 ∙ 0,16 = 38,6 м/с2


Вычисляем  = 86,2 ∙ 2 = 172,4 м/с2
= 86,2 ∙ 2 = 172,4 м/с2
Находим ускорение точки S3.

 = 5,62 ∙ 0,46 = 14,4 м/с2.
= 5,62 ∙ 0,46 = 14,4 м/с2.
 = 98,9 ∙ 0,46 = 45,5 м/с2
= 98,9 ∙ 0,46 = 45,5 м/с2


 = 23,9 ∙ 2 = 47,8 м/с2
= 23,9 ∙ 2 = 47,8 м/с2
 2020-01-14
2020-01-14 285
285








