Дивергенция векторного поля. Формула Остроградского–Гаусса в векторной форме

 

Пусть задано векторное поле

Дивергенцией или расходимостью векторного поля  называется скалярная функция, определяемая равенством:

На этот раз векторное поле  порождает скалярное поле .

С учетом понятий дивергенции и потока векторного поля формулу Остроградского–Гаусса можно представить в форме:

т. е. поток векторного поля  через замкнутую поверхность S в направлении внешней нормали равен тройному интегралу от дивергенции векторного поля по области, ограниченной этой поверхностью.

На основании формулы () можно записать:

 и, переходя к пределу, стягивая V в точку М (при этом величина V → 0), имеем:

 

То есть  есть предел отношения потока поля 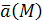 через бесконечно малую замкнутую поверхность, окружающую точку М, к величине объёма, ограниченного этой поверхностью. Из этого следует, что дивергенция не зависит от выбора системы координат.

Если поток

 то в область V втекает большее количество жидкости, чем вытекает из неё, т.е. внутри области V имеются источники жидкости.

Если П <0, то внутри области V есть стоки. Но поток векторного поля характеризует интенсивность источников и стоков лишь суммарно, т.е. при П ≥ 0 внутри области V могут быть как источники, так и стоки.

Для характеристики точки можно использовать .

Если 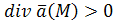, то данная точка есть источник, если  – то сток.

Заметим, что 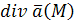 можно записать с помощью символического вектора Гамильтона

в следующем виде:

Свойства дивергенции:

1˚ Если  – постоянный вектор, то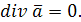

4˚ , U – скалярная функция.

 

Вихревой вектор поля. Формула Стокса в векторной форме

Вихревым вектором (вихрем), или ротором векторного поля

 называется вектор, имеющий координаты:

Тем самым векторное поле  порождает векторное поле вихря

Через символический вектор Гамильтона

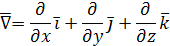
вихревой вектор записывается как векторное произведение вектора  на вектор поля , т. е.

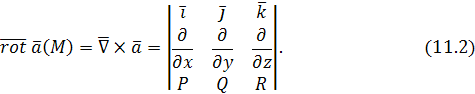
Как легко видеть, выражение

стоящее под знаком поверхностного интеграла в формуле Стокса, представляет собой скалярное произведение  вихря векторного поля  на единичный вектор нормали  к поверхности S.

Следовательно, формулу Стокса можно представить в векторной форме следующим образом:

Левая и правая части формулы () представляют, соответственно, циркуляцию векторного поля  и поток его вихря. Значит, формула Стокса утверждает: циркуляция векторного поля  по замкнутому контуру L равна потоку его вихря  через поверхность S, натянутую на этот контур.

Можно определить проекцию вектора  на любое направление  следующим образом:

 

т.е.  есть вектор, проекция которого на любое направление 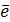 равна пределу отношения циркуляции векторного поля по контуру L плоской площадки τ, перпендикулярной этому направлению , к площади этой площадки, когда размеры этой площадки стремятся к нулю.

Или другими словами:  есть вектор, нормальный к поверхности, на которой плотность циркуляции достигает наибольшего значения.

Это, кроме прочего, означает и то, что вихрь поля (как и градиент, так и дивергенция) не зависит от выбора системы координат, а является характеристикой самого поля.

Отметим некоторые свойства ротора:

1˚ Если 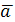– постоянный вектор, то

2˚

3˚

4˚ Если U – скалярная функция, а  – векторная, то

§4. СПЕЦИАЛЬНЫЕ ВЕКТОРНЫЕ ПОЛЯ

 

Векторное поле  называется соленоидальным, если во всех точках его дивергенция равна нулю, т.е. 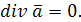 Примерами соленоидальных полей являются: поле скоростей вращающегося твердого тела; магнитное поле, создаваемое прямолинейным проводником, вдоль которого течет электрический ток, и т.д.

Векторное поле называется безвихревым, если его ротор тождественно равен нулю в области определения поля:

Векторное поле 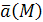 называется потенциальным, если оно является полем градиентов некоторой скалярной функции φ(M), т. е.   В этом случае функция φ (M) называется потенциалом поля.

Имеет место важное утверждение.

Теорема

Если векторное поле  непрерывно дифференцируемо в замкнутой односвязной области V, то каждое из следующих четырёх предложений равносильно любому другому из них:

ü – потенциальное поле;

ü – безвихревое поле;

ü циркуляция поля по любому замкнутому контуру, лежащему внутри области V, равна нулю;

ü криволинейный интеграл

не зависит от формы пути интегрирования.

Если φ(М) – потенциал поля, то потенциалом этого поля, как легко видеть, будет и любая другая функция вида ψ(М) = φ(М) + const.

Любой потенциал φ(М) поля  очевидно, можно представить в виде:

Отметим важное свойство указанных выше специальных векторных полей.

Теорема

Произвольное векторное поле  всегда может быть представлено в виде суммы потенциального поля  и соленоидального поля , т.е. .

Заметим, что для соленоидального поля можно определить векторный потенциал поля.

§5. ОПЕРАТОР ЛАПЛАСА. ГАРМОНИЧСЕКИЕ ФУНКЦИИ

 

Рассмотрим дифференциальную операцию второго порядка  где U – скалярная функция. Тогда

И так как 

 то скалярный квадрат записывают в виде:

и, следовательно

Подобно символическому оператору Гамильтона , можно ввести символический оператор:

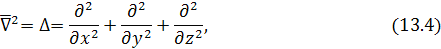
называемый оператором Лапласа.

Скалярная функция φ(x; y; z) называется гармонической в некоторой области, если она непрерывна в этой области вместе со своими производными   удовлетворяет уравнению

 

 

 

 ЗАКЛЮЧЕНИЕ

 

Векторный анализ — раздел математики, изучающий вещественный анализ векторов в двух или более измерениях. Методы векторного анализа находят большее применение в физике и инженерии.

Векторный анализ изучает векторные поля — функции из n -мерного векторного пространства в m -мерное — и скалярные поля — функции из n -мерного векторного пространства во множество скаляров.

Многие из результатов векторного анализа рассматриваются как частные случаи результатов из дифференциальной геометрии.

Для получения основных соотношений, используемых в векторном анализе, оказывается практически важным рассмотрение криволинейных и поверхностных интегралов, и их геометрических приложений. Так, например, теорема Стокса в векторной форме приобретает совершенно новый физический смысл.

Практически полезным является и введение оператора Гамильтона, с его помощью удобно записывать векторные операции первого порядка (градиент, дивергенция, ротор), а также комбинации со скалярными и векторными функциями. Для введения дифференциальных операций второго порядка используется оператор Лапласа. Дифференциальное уравнение Лапласа  играет важную роль в различных разделах математической физики.

К рассмотрению скалярных и векторных полей приводят многие задачи физики, электротехники, математики, механики и других технических дисциплин. Изучение одних физических полей способствует изучению и других. Математическим ядром теории поля являются рассмотренные нами понятия градиента, потока, потенциала, дивергенции, ротора, циркуляции и др. Эти понятия важны и в усвоении основных идей математического анализа функций многих переменных.

СПИСОК ЛИТЕРАТУРЫ:

 

1. Березанский Ю. М., Левитан Б. М.. Функциональный анализ/ http://www.cultinfo.ru/fulltext/1/001/008/117/905.htm

2. Бронштейн И.Н., Семендяев К.А. Справочник по математике для и инженеров и учащихся втузов. – М.: Наука, 1964. – 608 с.

3. Выгодский М.Я. Справочник по высшей математике. – М.: Наука, 1966. – 872 с.

4. Квальвассер В.И., Фридман М.И. Теория поля. Теория функций комплексного переменного. Операционное исчисление. – М.: Высшая школа, 1967. – 240 с.

5. Кузнецов Д.С. Специальные функции. – М.: Высшая школа, 1965. – 424 с.

6. Лекции по математическому анализу: Учеб. для вузов/ Г.И. Архипов, В.А. Садовничий, В.Н. Чубариков; Под ред. В.А. Садовничего. – 4-е изд., испр. – М.: Дрофа, 2004. – 640 с.

7. Ляшко И.И., Боярчук А.К., Гай Я.Г., Головач Г.П. Справочное пособие поп высшей математике. Т.3. Ч.2: Математический анализ: кратные и криволинейные интегралы. Изд. 6-е. – М.: КомКнига, 2007.

8. Магазинников Л.И. Функции комплексного переменного. Ряды. Интегральные преобразования. Учебное пособие. – Томск: Томский межвузовский центр дистанционного образования, 1999. – 205 с.

9. Панов В.Ф. Математика древняя и юная. – 2-е изд. – М.: Изд-во МГТУ им. Н.Э.Баумана, 2006.

10. Письменный Д.Т. – Ч.2 – 4-е изд. – М.: Айрис-пресс, 2006.

11. Фихтенгольц Г.М. Основы математического анализа. Т. 2. – М.: Государственное издательство технико-теоретической литературы, 1956. – 464 с.

12. Фихтенгольц Г.М. Курс дифференциального и интегрального исчисления. Т. 2. – М.: Наука, 1969. – 800 с.

13. www.wikipedia.ru