Поток векторного поля

Понятие потока векторного поля удобно рассматривать на примере потока жидкости, движущейся через некоторую поверхность. Объем жидкости, протекающей в единицу времени через поверхность, расположенную в движущейся жидкости, назовем потоком жидкости через эту поверхность.

Пусть поверхность S расположена в поле  скоростей частиц несжимаемой жидкости с плотностью ρ = 1. Можно показать, что поток векторного поля в этом случае равен

где  – единичный нормальный вектор к поверхности S, расположенный по одну сторону с вектором , а величина

Независимо от физического смысла вектора 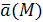 интеграл () по поверхности называют потоком векторного поля через поверхность S.

Пусть  и , тогда поток П вектора 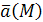 через поверхность S можно записать в виде:

Или учитывая связь поверхностных интегралов первого и второго родов, можно записать поток П через поверхностный интеграл в координатах: