Оператор Гамильтона и векторные дифференциальные операции второго порядка

 

Основные понятия векторного анализа: градиент, дивергенция, ротор - удобно представлять с помощью символического вектора ∇ («набла-вектор»)

 

 

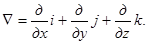
Правила действия с этим вектором:

. Произведение набла-вектора ∇ на скалярную функцию u(P) дает градиент этой функции:

 

 

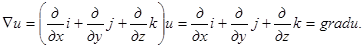
. Скалярное произведение набла-вектора ∇ на векторную функцию А(Р) дает дивергенцию этой функции:

 

 

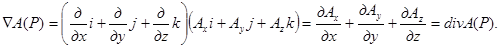
. Векторное произведение набла-вектора ∇ на векторную функцию А(Р) дает ротор этой функции:

 

 

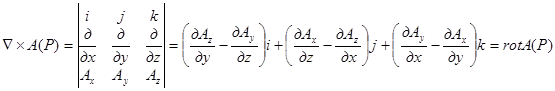
Таким образом действия с набла-вектором производятся по обычным правилам действий векторной алгебры, а затем умножением, скажем д/дx на скалярную функцию заменяется производной этой функции по x. Набла-вектор называют ещё оператором Гамильтона.

Действия взятия градиента, дивергенции, ротора будут векторными дифференциальными операциями первого порядка. В них участвуют только первые производные от скалярных функций.

Векторные дифференциальные операции второго порядка.

Пусть имеется скалярное поле u(P) и мы нашли градиент этого поля grad u. Поле градиента является векторным полем, и мы можем искать его дивергенцию и ротор: div grad u и rot grad u.

Если имеется векторное поле A(P)=A_xi+A_yj+A_zk, то оно порождает два поля: скалярное поле divA(P) и векторное поле rotA(P). Следовательно мы можем находить градиент первого поля: grad divA(P), дивергенцию и ротор второго поля: div rotA(P) и rot rotA(P). Всего мы имеем пять векторных дифференциальных операций второго порядка. Особенно важными являются три из них, которые рассмотрим подробнее.

 

а)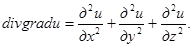

 

Действительно, 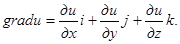 Образуя дивергенцию этого вектора, мы получаем написанное равенство. Правая часть его называется оператором Лапласа от функции u и обозначается ∆u

 

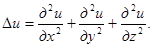
Выражение div grad u можно с помощью набла-вектора записать ещё и так: div grad u=∇ (∇u)= ∇²u

Это обозначение оператора Лапласа тоже часто употребляется.

 

б) rot grad u=0

 

Соотношение это проверяется совсем просто. Каждая скобка в выражении для ротора представляет в этом случае разность вторых смешанных производных функции и, отличающихся лишь порядком дифференцирования, например:

 

 

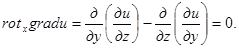
С помощью набла-вектора это соотношение записывается так:

 

rot grad u= ∇x (∇u)=(∇x ∇) u=0

 

так как векторное произведение одинаковых «векторов» равно нулю.

 

в) div rot A(P)=0

 

Образуя дивергенцию от rot A(P), получим

 

 

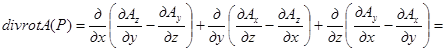
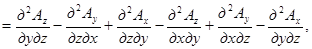
что в силу равенства вторых смешанных производных равно нулю.

Если записать доказываемое соотношение с помощью набла-вектора;

 

div rot A(P)=∇ (∇xA),

 

то получим смешанное произведение трех «векторов», из которых два вектора одинаковы. Но такое произведение равно нулю.

 

г) rot rot A(P)=grad div A(P) - ∆A(P),

где ∆A(P)=∆A_xi+∆A_yj+∆A_zk (∆ - оператор Лапласа).

 

Виды векторных полей