Электромагнитное поле

 

Одним из важнейших приложений введенных нами понятий векторного анализа является изучение электромагнитных полей. Мы рассмотрим несколько простых примеров.

Электрическое поле

Пусть Е - поле напряженности точечного заряда q, помещенного в начало координат. Напряженность поля в точке P (x, y, z) равна

 

,

 

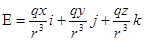где 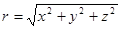 - расстояние от точки Р до начала координат. Векторными линиями такого поля служат лучи, выходящие из начала координат, то есть из заряда.

Поле напряженности Е является полем потенциальным. Обычно за потенциал φ поля Е берут функцию 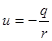, взятую с противоположным знаком: .

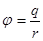Таким образом, разность потенциалов между двумя точками поля равна взятой с противоположным знаком работе, совершаемой силами поля при перемещении единичного положительного заряда из одной точки во вторую. Легко проверить, что .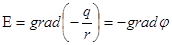

Это значит также, что rot E = - rot grad φ = 0.

Найдем дивергенцию поля напряженности. Имеем

 

, , .

 

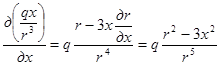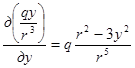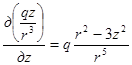Отсюда

 

.

 

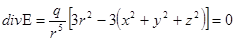Следовательно,

Поток вектора Е через любую замкнутую поверхность, не содержащую внутри себя начала координат, равен нулю.

Если же начало координат, то есть заряд, содержится внутри поверхности, то такого вывода сделать уже нельзя, так как в начале координат поле не определено.

Вычислим поток вектора Е через сферу радиуса R с центром в начале координат. На поверхности этой сферы направление вектора Е совпадает с направлением нормали, то есть радиуса вектора. Поэтому

 

.

 

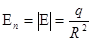Отсюда поток К равен

 

.

 

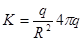Мы видим, что величина потока не зависит от радиуса сферы R. Легко показать, что величина потока остается неизменной для любой замкнутой поверхности, окружающей начало координат.

 

 

Рис. 2.2. Произвольная поверхность с помещенной в неё сферой

 

Так как часть конуса, заключенная между участком сферы и данной поверхностью, является векторной трубкой, а дивергенция поля равна нулю, то потоки через участки сферы и поверхности равны между собой. Складывая потоки через все такие участки поверхности, получаем, что поток вектора Е через любую поверхность, окружающую начало координат равен потоку через сферу, то есть 4πq. Будем считать, что внутренняя сфера имеет радиус, равный единице. Тогда поток через участок поверхности S₁ (рис.) будет равен qω, где ω - площадь поверхности сферы единичного радиуса, в которую проецируется участок поверхности. Величину ω называют телесным углом, под которым поверхность S₁ видна из начала координат.

Пусть теперь поле создано системой электрических зарядов 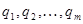. Обозначим через E_i напряженность поля, создаваемого зарядом q_i, а через Е - результирующую напряженность.

Тогда

 

.

 

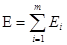Проекция вектора Е на направление нормали n к любой поверхности равна

.

 

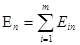Стало быть, поток через поверхность равен

 

,

 

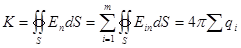причем последняя сумма распространена только на те заряды q_i, которые лежат внутри рассматриваемой поверхности. Эта формула, играющая важную роль в изучении электрических полей, называется электростатической теоремой Гаусса.

Пусть мы имеем дело с непрерывным распределением заряда. Обозначим через ρ плотность распределения заряда. Если плотность заряда непостоянна, то ρ является функцией точки поля Р, то есть её координат. Суммарный заряд в данном объеме Ω будет равен .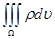

Применив к этому заряду теорему Гаусса, получим

 

,

 

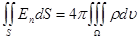где S - граница области Ω.

Преобразуем первый интеграл, вводя div E:

 

.

 

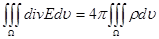Отсюда

 

.

 

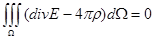Поскольку интеграл равен нулю для любой области интегрирования Ω, то получим .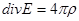

Примем без доказательства, что свойство электрического поля быть потенциальным сохраняется при непрерывном распределении зарядов.

Обозначим его потенциал через φ; тогда Е=-grad φ. Тогда

 

div E=-div grad φ=-Δφ.

 

Из вышеприведенных равенств получим

 

.

 

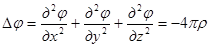Полученное уравнение называется уравнением Пуассона. В трех точках поля, где плотность заряда ρ равна нулю, оно превращается в уравнение Лапласа: Δφ=0.