2020-04-20
127
Пусть магнитное поле создано постоянным током I, текущим по бесконечному прямолинейному проводнику. Найдем вектор напряженности магнитного поля, создаваемого этим током. Согласно закона Био-Савара элемент тока создает в данной точке напряженность магнитного поля, равную по величине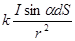 
, где I - ток, dS - элемент длины проводника, r - расстояние от элемента тока до рассматриваемой точки, α - угол между направлением тока и прямой, соединяющей точку, в которой ищется поле, и элементом тока, k - коэффициент пропорциональности, зависящий от выбора системы единиц. Вектор напряженности направлен по нормали к плоскости, содержащей элемент тока и точку наблюдения; направление напряженности устанавливается правилом Ампера. В векторной форме закон Био-Савара записывается так:
,
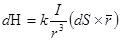где dН - вектор напряженности поля, создаваемого элементом тока, dS - вектор, направленный по проводнику, а r - вектор, проведенный из элемента тока в точку М, в которой ищется напряженность.
Обозначим переменное расстояние от элемента тока до начала координат через ξ, а координаты точки М через x, y, z. Тогда
, 
,
,
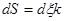где 
- расстояние от точки М до провода. Вычисляя векторное произведение, находим dH:
.
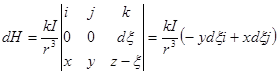Отсюда
,
, 
.
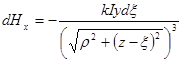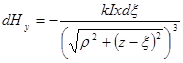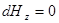Чтобы найти Hx и Hy, проинтегрируем выражение для их дифференциалов в пределах от - ∞ до ∞. Для этого вычислим несобственный интеграл
.
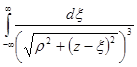Подстановка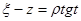 
, 
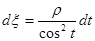приводит к интегралу
.
Поэтому
, 
, 
.
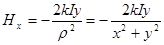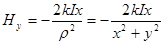В точках оси Oz поле не определено. Таким образом, вектор напряженности Н имеет то же направление, что и вектор линейной скорости при вращении тела вокруг оси Oz, если направление тока совпадает с направлением вектора угловой скорости. Модуль вектора Н равен
.
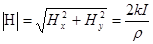Легко проверить, что дивергенция поля равна нулю. Имеем
, 
, 
.
Следовательно,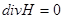 
.
Ротор этого поля также во всех точках равен нулю. Для этого надо только проверить равенство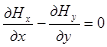 
.
Следовательно, циркуляция поля по любому контуру, не окружающему ось Oz, равна нулю. Если же контур окружает ось Oz (рис. 2.5.), то такого вывода сделать нельзя, поскольку такой контур невозможно заключить в односвязную область, не содержащую точек оси Oz, в которых поле не определено.
Вычислим циркуляцию по окружности радиуса R, лежащей в плоскости Oxy, с центром в начале координат
x=R cos t, y=R sin t.
Тогда
.
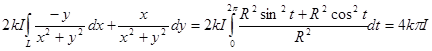Рис. 2.5. Положение контура относительно осей координат
Величина циркуляции не зависит от радиуса окружности R. Можно доказать, что она остается одной и той же для любого контура, окружающего ось Oz.
