| И 3.27 | Действующее значение синусоидального напряжения на конденсаторе пропорционально действующему значению синусоидального тока
 . .
|
Это утверждение следует из формулы (3.13), если учесть соотношения (3.6) и (3.7) между амплитудами и действующими значениями синусоидальных функций.
Коэффициент пропорциональности между напряжением и током в последней формуле 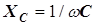 играет роль сопротивления и имеет его размерность
играет роль сопротивления и имеет его размерность
 Ом
Ом  Ом.
Ом.
| И 3.28 | Определение. Величина
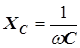 (3.14)
называется емкостным сопротивлением конденсатора в цепи переменного синусоидального тока; (3.14)
называется емкостным сопротивлением конденсатора в цепи переменного синусоидального тока;
 . (3.15) . (3.15)
|
Емкостное сопротивление конденсатора обратно пропорционально частоте протекающего через него тока.
Реактивная мощность конденсатора
Если начальную фазу тока принять равной 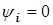 , как на рис. 3.2, то мгновенная мощность конденсатора равна
, как на рис. 3.2, то мгновенная мощность конденсатора равна
 .
.
Средняя за период мощность равна
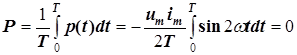 .
.
| И 3.29 | Конденсатор не потребляет электрической энергии. Он обменивается электрической энергией с другими элементами цепи с частотой, вдвое большей, чем частота тока. |
Спустя 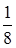 периода после начала очередного периода тока, например, в момент времени
периода после начала очередного периода тока, например, в момент времени  на рис. 3.2 мгновенная мощность конденсатора принимает минимальное значение
на рис. 3.2 мгновенная мощность конденсатора принимает минимальное значение
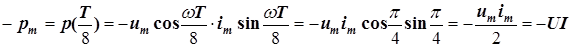 .
.
Если напряжение выразить через ток в соответствии с формулой (3.15), то
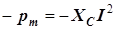 .
.
| И 3.30 | Определение. Величина
 называется реактивной мощностью конденсатора (очевидно, что
называется реактивной мощностью конденсатора (очевидно, что  ). ).
|
ПОСЛЕДОВАТЕЛЬНОЕ ВКЛЮЧЕНИЕ РЕЗИСТОРА,
КАТУШКИ И КОНДЕНСАТОРА
 2020-04-07
2020-04-07 193
193








