Пусть в некотором узле электрической цепи выполняется следующее соотношение между токами
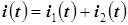 ,
,
где 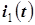 и
и 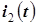 - известные синусоидальные токи:
- известные синусоидальные токи:
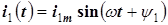 ,
,
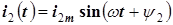 .
.
Ток 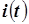 можно определить по формулам тригонометрии. Это можно сделать и с помощью комплексных чисел. Сопоставим синусоидальным токам
можно определить по формулам тригонометрии. Это можно сделать и с помощью комплексных чисел. Сопоставим синусоидальным токам 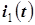 и
и 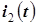 комплексные токи
комплексные токи 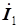 и
и 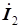 , затем найдем сумму комплексных токов
, затем найдем сумму комплексных токов 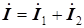 и, наконец, найдем синусоидальный ток
и, наконец, найдем синусоидальный ток 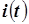 , соответствующий комплексному току
, соответствующий комплексному току 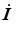 . В обоих случаях получается один и тот же результат.
. В обоих случаях получается один и тот же результат.
Эквивалентность двух способов, которыми можно вычислить сумму синусоидальных токов, можно иллюстрировать следующей схемой:
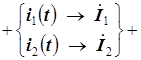
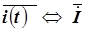
Символ взаимно однозначного соответствия синусоидальных и комплексных токов 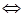 в нижней строке схемы показывает, что по этой схеме можно определять не только сумму синусоидальных токов, но и сумму комплексных токов, соответствующих заданным синусоидальным токам. Число слагаемых в этой схеме (то есть число синусоидальных токов и соответствующих им комплексных токов) можно увеличить и перед каждым слагаемым поставить плюс или минус. Тогда получается, что любой алгебраической сумме синусоидальных токов можно поставить в соответствие аналогичную сумму комплексных токов и результаты суммирования соответствуют друг другу (по правилам И 4.3).
в нижней строке схемы показывает, что по этой схеме можно определять не только сумму синусоидальных токов, но и сумму комплексных токов, соответствующих заданным синусоидальным токам. Число слагаемых в этой схеме (то есть число синусоидальных токов и соответствующих им комплексных токов) можно увеличить и перед каждым слагаемым поставить плюс или минус. Тогда получается, что любой алгебраической сумме синусоидальных токов можно поставить в соответствие аналогичную сумму комплексных токов и результаты суммирования соответствуют друг другу (по правилам И 4.3).
| И 4.4 | Теорема. Если синусоидальным токам 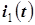 , , 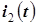 ,..., ,..., 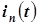 соответствуют комплексные токи соответствуют комплексные токи 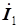 , , 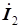 , …, , …, 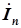 , то сумме синусоидальных токов, то есть току , то сумме синусоидальных токов, то есть току
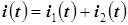 +…+ +…+ 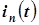 ,
соответствует сумма комплексных токов, то есть комплексный ток ,
соответствует сумма комплексных токов, то есть комплексный ток
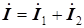 +…+ +…+ 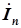 . .
|
Доказательство связано с громоздкими выкладками и не содержит поучительных идей. Ниже оно приводится для случая, когда суммируются два тока.
Заданные токи 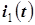 и
и 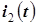 по теореме о синусе суммы можно представить в виде линейной комбинации функций
по теореме о синусе суммы можно представить в виде линейной комбинации функций 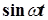 и
и 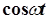 , и после этого найти сумму токов, которая также оказывается линейной комбинацией синусоиды и косинусоиды. Эту линейную комбинацию по формулам (3.18) и (3.19) можно преобразовать в синусоиду с некоторой начальной фазой
, и после этого найти сумму токов, которая также оказывается линейной комбинацией синусоиды и косинусоиды. Эту линейную комбинацию по формулам (3.18) и (3.19) можно преобразовать в синусоиду с некоторой начальной фазой
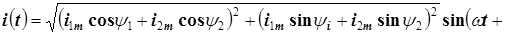
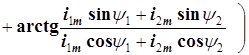 .
.
Соответствующий комплексный ток равен
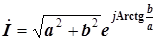 ,
,
где использованы сокращенные обозначения
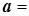
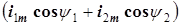 /
/ 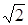 ,
,
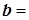
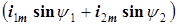 /
/ 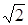 .
.
 Теперь найдем комплексный ток
Теперь найдем комплексный ток 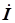 другим путем. Сначала определим комплексные токи, соответствующие токам
другим путем. Сначала определим комплексные токи, соответствующие токам 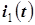 и
и 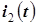 ,
,

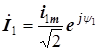 ,
, 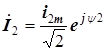 .
.
Затем найдем сумму комплексных токов, предварительно представив их в алгебраической форме,
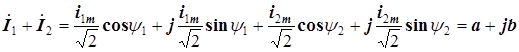 .
.
После преобразования последнего выражения в показательную форму, получается, что
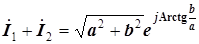
Легко убедиться, что
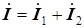 ,
,
то есть оба способа вычисления комплексного тока 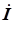 дают один и тот же результат.
дают один и тот же результат.
 2020-04-07
2020-04-07 580
580








