Комплексное напряжение

Символический метод расчета

Электрических цепей переменного

Синусоидального тока

КОМПЛЕКСНЫЕ ТОКИ И НАПРЯЖЕНИЯ

Математическое введение (формула Эйлера)

Между синусоидальными и экспоненциальными (показательными) функциями существует простая зависимость, которая получила название формулы Эйлера,

,

где  - мнимая единица. В частности, если ,

то

или

.

Формула Эйлера применяется для перевода комплексных чисел из показательной формы в алгебраическую. В показательной форме комплексное число содержит модуль z и аргумент :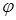

.

В алгебраической форме комплексное число имеет действительную часть x и мнимую часть y:

.

Очевидно, что

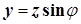, .                             (4.1)

Решив эти уравнения относительно  и 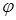, получаем формулы для перевода комплексных чисел из алгебраической формы в показательную

, .                      (4.2)

В задачах электротехники пределы изменения 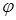 обычно выбирают в пределах от до и вычисляют по формуле

Для запоминания формул (4.1) и (4.2), предназначенных для перевода комплексных чисел из одной формы записи в другую, можно использовать треугольник, похожий на треугольник сопротивлений (рис. 4.1).

Рис. 4.1. Треугольник, иллюстрирующий зависимости между действительной и мнимой частями комплексного числа, с одной стороны, и его модулем и аргументом, с другой стороны

Комплексный ток

В электрической цепи с источником синусоидального напряжения протекают синусоидальные токи. Пусть один из них равен

,

где I - действующее значение тока. Запишем соответствующую косинусоидальную функцию

.

Затем с помощью формулы Эйлера составим комплексную функцию

.

Множитель  одинаков для всех токов цепи. Комплексное число 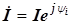 характеризует ток рассматриваемой ветви.

И 4.1

Определение. Комплексное число 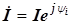называют комплексным током. Модуль комплексного тока равен действующему значению синусоидального тока, аргумент комплексного тока – начальной фазе синусоидального тока.

Комплексное напряжение

Синусоидальному напряжению можно сопоставить комплексное напряжение аналогично тому, как синусоидальному току был поставлен в соответствие комплексный ток:

.

Здесь U – действующее значение напряжения;  - его начальная фаза.

И 4.2

Определение. Комплексное число называют комплексным напряжением. Модуль комплексного напряжения равен действующему значению синусоидального напряжения, аргумент комплексного напряжения – начальной фазе синусоидального напряжения.

Преобразование синусоидальных токов и напряжений в комплексные числа (комплексные токи и напряжения) позволяет преобразовать тригонометрические уравнения, составленные по законам Кирхгофа для синусоидальных токов и напряжений, в алгебраические уравнения для комплексных токов и напряжений. Благодаря тому, что в уравнениях для комплексных токов можно опустить множитель , общий для всех токов, решение алгебраических уравнений оказывается не столь громоздким, как решение тригонометрических уравнений. Решив систему уравнений Кирхгофа относительно комплексных токов, можно затем по комплексным токам определить синусоидальные токи.