Определение 1. Произведение 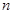 первых натуральных чисел называется факториалом числа
первых натуральных чисел называется факториалом числа 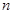 и обозначается символом
и обозначается символом 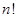 (читается «эн факториал»).
(читается «эн факториал»).
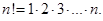 (1)
(1)
Приведем некоторые значения факториала:
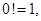
| 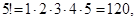
|
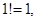
| 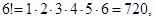
|

| 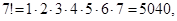
|

| 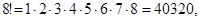
|
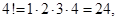
| 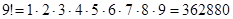
|
Рассмотрим  множеств
множеств 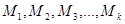 , содержащих по
, содержащих по 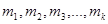 элементов соответственно. Выбирается по одному элементу из каждого множества и составляется еще одно множество. Число способов, которыми можно выбрать по одному элементу из каждого множества, равно произведению
элементов соответственно. Выбирается по одному элементу из каждого множества и составляется еще одно множество. Число способов, которыми можно выбрать по одному элементу из каждого множества, равно произведению 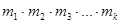 . В этом состоит принцип произведения комбинаторики.
. В этом состоит принцип произведения комбинаторики.
В задачах теории вероятностей часто рассматриваются различные соединения (комбинации, наборы)  элементов из множества, содержащего
элементов из множества, содержащего 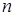 элементов
элементов  . Будем рассматривать такие соединения, в которые каждый элемент данного множества может входить не более одного раза, то есть соединения без повторений. Рассмотрим три вида соединений: размещения, перестановки, сочетания.
. Будем рассматривать такие соединения, в которые каждый элемент данного множества может входить не более одного раза, то есть соединения без повторений. Рассмотрим три вида соединений: размещения, перестановки, сочетания.
Определение 2. Размещениями из 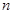 элементов по
элементов по 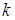 элементов называются наборы
элементов называются наборы  элементов, отличающиеся один от другого или самими элементами (составом элементов), или их порядком. Число размещений обозначается
элементов, отличающиеся один от другого или самими элементами (составом элементов), или их порядком. Число размещений обозначается 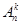 .
.
Число размещений из 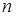 элементов по
элементов по  элементов находится по формуле:
элементов находится по формуле:
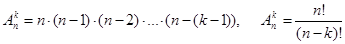 . (2)
. (2)
Определение 3. Перестановками из данных 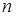 элементов называются наборы из
элементов называются наборы из 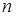 элементов, отличающиеся только их порядком.
элементов, отличающиеся только их порядком.
Перестановки – это частный случай размещений. Число всех перестановок обозначают символом 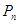 . Число
. Число 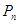 найти несложно. Для этого в формулу (2) подставляем
найти несложно. Для этого в формулу (2) подставляем 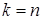 .
.

Определение 4. Сочетаниями, содержащими  элементов, выбранных из
элементов, выбранных из 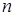 элементов заданного множества, называются всевозможные наборы
элементов заданного множества, называются всевозможные наборы 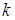 элементов, различающиеся хотя бы одним элементом. Число сочетаний из
элементов, различающиеся хотя бы одним элементом. Число сочетаний из 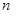 элементов по
элементов по 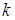 элементов обозначают
элементов обозначают 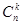 или
или 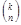 .
.
Число сочетаний из 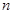 элементов по
элементов по  элементов находится по формуле:
элементов находится по формуле:
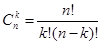 .
.
 2020-04-20
2020-04-20 143
143








