2020-04-20
206
Вероятность появления одного из двух несовместных событий, безразлично какого, равна сумме вероятностей этих событий.
Следствие: вероятность появления одного из нескольких попарно несовместных событий, безразлично какого, равна сумме вероятностей этих событий.
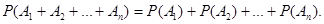
Пример. В ящике 15 деталей, среди которых 5 окрашенных. Сборщик наудачу достает 3 детали. Найти вероятность того, что из трех взятых деталей окрашенной окажется хотя бы одна деталь.
Решение. Требование – хотя бы одна из трёх деталей окрашена – будет осуществлено, если произойдет любое из следующих 3 несовместных событий: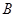 
– одна деталь из трех окрашена, 
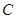– две детали из трех окрашены, 
– три детали окрашены. Интересующее нас событие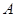 
можно представить в виде суммы событий: 
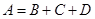, и по теореме о вероятности суммы несовместных событий получаем
;
;
;
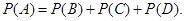
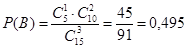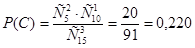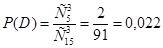тогда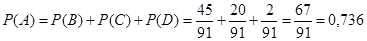 
.
(Если сложить числа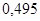 
, 
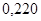и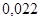 
, то получится 
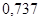, что не равно 
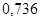. Погрешность получается в результате округлений.)
Определение 3. Два события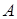 
и 
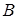называются независимыми, есливероятность появления одного из них не меняется от появления или не появления другого и наоборот. В противном случае события называются зависимыми.
Пример. Рассмотрим две урны с шарами. В каждой урне по 5 красных и 6 синих шаров. Из каждой урны один за другим вынимаются два шара, но в первой урне шары возвращаются (выбор с возвратом), а во второй урне не возвращаются (выбор без возврата). Рассмотрим событие 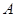– второй вынутый из урн шар красный. В первом случае (с возвратом) вероятность события 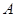не зависит от того, каким был вынут первый шар (красный или синий), а во втором случае (без возврата) вероятность события 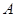зависит от того, какой был вынут первый шар (красный или синий).
Условную вероятность появления события 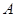при условии, что произошло событие 
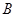, обозначим символом: 
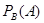или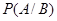 
.
Определение 4. Произведением двух событи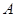й и 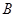называют событие 
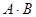, состоящее в совместном появлении этих событий. Произведением нескольких событий называют событие, состоящее в совместном появлении всех этих событий.
