Определение 1. Интервальной называют оценку, которая определяется двумя числами – концами интервала, покрывающего оцениваемый параметр.
Доверительным называют интервал, который с заданной вероятностью (надежностью) 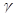 покрывает заданный параметр.
покрывает заданный параметр.
Интервальной оценкой с надежностью 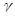 математического ожидания
математического ожидания 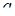 нормально распределенного признака
нормально распределенного признака  по выборочной средней
по выборочной средней  при известном среднем квадратическом отклонении
при известном среднем квадратическом отклонении 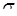 генеральной совокупности служит доверительный интервал
генеральной совокупности служит доверительный интервал
 ,
,
где  – точность оценки,
– точность оценки,
 – объем выборки,
– объем выборки,
 – значение аргумента функции Лапласа
– значение аргумента функции Лапласа  (см. приложение 2), при котором
(см. приложение 2), при котором  .
.
При неизвестном  (и объеме выборки
(и объеме выборки  ) доверительным будет интервал
) доверительным будет интервал
 ,
,
где  – «исправленное» выборочное среднее квадратическое отклонение,
– «исправленное» выборочное среднее квадратическое отклонение,  находят по таблице приложения 3 по заданным значениям
находят по таблице приложения 3 по заданным значениям  и
и  .
.
Интервальной оценкой с надежностью  среднего квадратического отклонения
среднего квадратического отклонения  нормально распределенного количественного признака
нормально распределенного количественного признака  по «исправленному» выборочному среднему квадратическому отклонению
по «исправленному» выборочному среднему квадратическому отклонению  служит доверительный интервал:
служит доверительный интервал:
 при
при 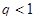 ,
,
 при
при  ,
,
где  находят по таблице приложения 4 по заданным
находят по таблице приложения 4 по заданным  и
и  .
.
Интервальной оценкой с надежностью  неизвестной вероятности
неизвестной вероятности 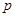 биномиального распределения по относительной частоте
биномиального распределения по относительной частоте  служит доверительный интервал (с приближенными концами
служит доверительный интервал (с приближенными концами  и
и  ):
):
 ,
,
где
 ,
,
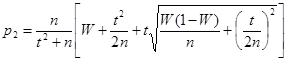 .
.
где  – общее число испытаний,
– общее число испытаний,
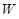 – относительная частота, равная отношению
– относительная частота, равная отношению 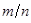 (
( – число появлений
– число появлений
события);
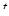 – значение аргумента функции Лапласа (приложение 2), при котором
– значение аргумента функции Лапласа (приложение 2), при котором  (
( – заданная надежность).
– заданная надежность).
Замечание. При больших значениях  (порядка сотен) можно принять в качестве приближенных границ доверительного интервала
(порядка сотен) можно принять в качестве приближенных границ доверительного интервала
 ,
,  .
.
Пример 1. Из генеральной совокупности извлечена выборка объема  :
:
Варианта 
| 2 | 3 | 5 | 7 | 10 | 13 |
Частота 
| 2 | 4 | 7 | 8 | 3 | 1 |
Требуется оценить с надежностью 0,95 математическое ожидание нормально распределенного признака генеральной совокупности по выборочной средней при помощи доверительного интервала.
Решение. Выборочную среднюю и «исправленное» среднее квадратическое отклонение найдем соответственно по формулам
 ,
, 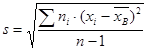 .
.
Подставим в эти формулы данные задачи:
 ,
,

Таким образом, получим  ,
, 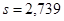 .
.
Найдем искомый доверительный интервал:
 .
.
Значение  находят по таблице приложения 3 по заданным
находят по таблице приложения 3 по заданным  и
и 

 :
:  .
.
Подставляя 
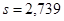 ;
;  ; получим
; получим
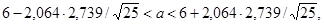
 .
.
Получили доверительный интервал  , покрывающий неизвестное математическое ожидание
, покрывающий неизвестное математическое ожидание  с надежностью
с надежностью 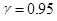 .
.
Пример 2. По данным выборки объема 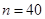 из генеральной совокупности найдено «исправленное» среднее квадратическое отклонение
из генеральной совокупности найдено «исправленное» среднее квадратическое отклонение  нормально распределенного количественного признака. Найти доверительный интервал, покрывающий генеральное среднее квадратическое отклонение
нормально распределенного количественного признака. Найти доверительный интервал, покрывающий генеральное среднее квадратическое отклонение  с надежностью 0,99.
с надежностью 0,99.
Решение. Задача сводится к отысканию доверительного интервала
 (если
(если  ) или
) или  (если
(если  ).
).
Значение  находят по таблице приложения 4 по заданным
находят по таблице приложения 4 по заданным  и
и 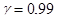 :
:  . Так как
. Так как 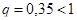 , то воспользуемся первым соотношением. Подставим
, то воспользуемся первым соотношением. Подставим  и
и  . Получим
. Получим
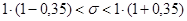 ,
,
отсюда
 .
.
Таким образом, полученный доверительный интервал  покрывает неизвестное среднее квадратическое отклонение
покрывает неизвестное среднее квадратическое отклонение  с надежностью (доверительной вероятностью)
с надежностью (доверительной вероятностью)  .
.
Часто используют также следующие выборочные характеристики.
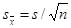 – ошибка средней (среднее квадратическое отклонение выборочной средней от генеральной средней);
– ошибка средней (среднее квадратическое отклонение выборочной средней от генеральной средней);
 – коэффициент вариации (доля среднего квадратического отклонения в выборочной средней, в процентах).
– коэффициент вариации (доля среднего квадратического отклонения в выборочной средней, в процентах).
 2020-04-20
2020-04-20 427
427








