Точечные оценки параметров распределения

Определение  1. Статистической оценкой  неизвестного параметра 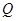 теоретического распределения называют функцию  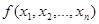от наблюдаемых  значений  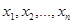количественного признака .

Определение 2. Точечной оценкой называют статистическую оценку, которая определяется одним числом 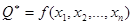, где 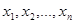─ результаты 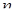наблюдений над количественным признаком (выборка).

Определение 3. Несмещенной называют точечную оценку , математическое ожидание которой равно оцениваемому параметру 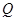 при любом объеме выборки, то есть 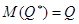. Смещенной называют точечную оценку, математическое ожидание которой не равно оцениваемому параметру.

Рассмотрим основные точечные оценки параметров распределения.

Выборочная средняя.

Пусть для изучения генеральной совокупности относительно количественного признака 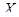 извлечена выборка объема .

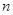Определение 4. Выборочной средней 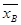 называют среднее арифметическое значение признака выборочной совокупности.

Если все значения 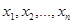 признака выборки объема  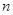различны, то выборочная средняя находится по формуле:

.

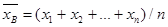Если же все значения признака 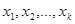 имеют соответственно частоты 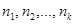, причем  объем выборки 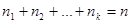, то

.

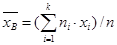Выборочная средняя является несмещенной оценкой генеральной средней (неизвестного математического ожидания).

 Замечание. Если первоначальные варианты 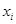 ─ большие числа, то для упрощения решения целесообразно вычесть из каждой варианты одно и то же число 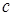, то есть перейти к условным вариантам 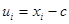. Тогда

.