2020-04-20
214
Смещенной оценкой генеральной дисперсии служит выборочная дисперсия. Эту величину вводят для того, чтобы охарактеризовать рассеяние наблюдаемых значений количественного признака 
выборки вокруг среднего значения 
.
Определение 5. Выборочной дисперсией 
называют среднее арифметическое квадратов отклонения наблюдаемых значений признака от их среднего значения 
.
Если все значения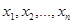 
признака выборки объема 
различны, то выборочная дисперсия находится по формуле:
Если значения признака 
имеют соответственно частоты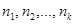 
, причем 
, то
Эта оценка является смещенной, так как 
, где 
– генеральная дисперсия.
Теорема. Выборочная дисперсия равна среднему квадратов значений признака минус квадрат выборочной средней.
.
Для вычисления выборочной дисперсии эта формула наиболее удобна.
Замечание. Если перейти к условным вариантам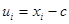 
, то дисперсия при этом не изменится. Тогда
