Система наведения по лучу с использованием метода трех точек

В системе наведения по лучу, в отличии от ТУ-1, при использовании метода трех точек сигналы управления и вычисляются по формулам (2.19).

Нелинейная математическая модель для исследования динамики данной системы наведения в пространстве отличается от системы уравнений, рассмотренной в разделе 3.1, только тем, что уравнения (3.4). (3.5), (3.6) нужно заменить формулами (2.19) и соотношениями для вычисления и .

Рассмотрим математическую модель для исследования наведения по лучу в горизонтальной плоскости. Используя уравнения (2.3), первое уравнение системы (2.19) и математические модели элементов системы наведения получим следующую систему уравнений:

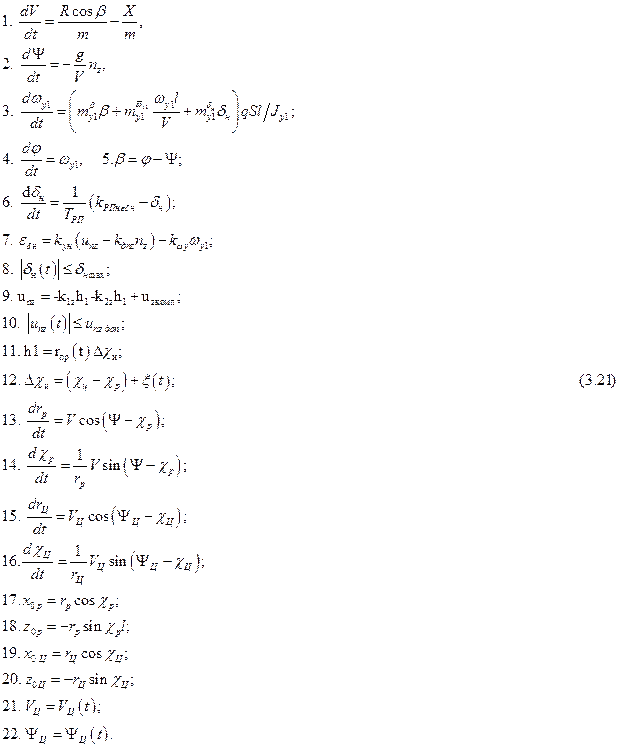
где ; ; .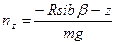

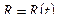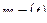Здесь - программное изменение расстояния ЛА от КПУ;

- ошибка бортового радиолокационного устройства измерения .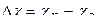

Рассмотрим также линейную математическую модель при наведении по лучу в горизонтальной плоскости.

Линейная система уравнений (2.13) определяет динамику контура стабилизации перегрузки в горизонтальной плоскости. Этой системе уравнений соответствует структурная схема, приведенная на рис. 2.4.

Из кинематических уравнений

можно получить передаточную функцию кинематического звена, аналогичную (3.17).

Упрощенная передаточная функция имеет вид

где длина дуги , .

Передаточную функцию для команды управления в горизонтальной плоскости можно записать на основе (2.19) в следующем виде:

Записывая передаточные функции для линейных моделей элементов, составим структурную схему системы наведения по лучу в горизонтальной плоскости, приведенную на рис. 3.9.

На рисунке пунктирной линией показано радиолокационное измерительное устройство, которое измеряет угловую ошибку 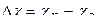. Возмущение 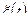на выходе этого устройства показано стрелочкой.