Задания 1 - 4 относятся к разделу «Обыкновенные дифференциальные уравнения». Следует разобрать основные определения теории и методы решения основных типов дифференциальных уравнений первого порядка.
Пример 1. Найти общее решение дифференциального уравнения с разделяющимися переменными:
 .
.
Решение. Общий вид уравнения с разделяющимися переменными следующий:
 ,
,
либо в терминах дифференциалов
 .
.
Характерно, каждое из слагаемых – произведение функций, зависящих только от одной переменной. Делением обеих частей уравнения его приводим к виду с разделенными переменными. Например, в левой части преобразованного уравнения отсутствует переменная  , а в правой – переменная
, а в правой – переменная  :
:
 .
.
Интегрируя затем левую и правую часть, получим общее решение в неявном виде (общий интеграл). Итак,
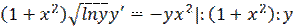




Окончательно, общий интеграл имеет вид:
 , где
, где
С – произвольная постоянная.
Пример 2. Решить однородное уравнение: 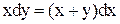 .
.
Обыкновенное дифференциальное уравнение называется однородным если при замене  , а
, а  оно не меняется.
оно не меняется.
Другими словами, если уравнение можно привести к виду
 где f – любая функция, то оно является однородным.
где f – любая функция, то оно является однородным.
Однородное уравнение приводится к уравнению с разделяющимися переменными типа с помощью подстановки  .
.
Покажем, что это уравнение однородное. Для этого поделим его обе части на  .
.
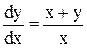
Или, поделив почленно правую часть на x:
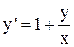 .
.
Слева стоит производная y, а справа функция, зависящая только от 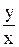 . Уравнение является однородным. Применим подстановку
. Уравнение является однородным. Применим подстановку
 .
.
Получим:

Сократим на u и поделим на x:




Возвращаясь к исходной неизвестной функции 

 .
.
Кроме этого, есть еще решение  , которое было потеряно при делении на x.
, которое было потеряно при делении на x.
В 3-ем задании рассматривается линейное ДУ первого порядка.
Если обыкновенное дифференциальное уравнение можно привести к виду
 ,
,
где p(x) и q(x) функции, не зависящие от y, а только от переменной x, то такое уравнение называется линейным (относительно y).
Линейные ОДУ первого порядка можно решать с помощью подстановки Бернулли
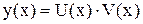 ,
,
где U(x) и V(x) две новые неизвестные функции, одна из их лишняя. Её можно выбирать по своему усмотрению. Найдем теперь производную  по правилу дифференцирования произведения:
по правилу дифференцирования произведения:

Подставив выражения для y и y' в уравнение, получим:

Распорядимся произволом так, чтобы исходное уравнение «расщепилось» на два простых:

Теперь видно, что если положить  , то оставшееся уравнение приобретет простой вид. Таким образом, исходное уравнение распадается на два уравнения, каждое из которых является уравнением с разделяющимися переменными:
, то оставшееся уравнение приобретет простой вид. Таким образом, исходное уравнение распадается на два уравнения, каждое из которых является уравнением с разделяющимися переменными:


Теперь, найдя из первого уравнения какую-либо функцию V(x), подставим ее во второе и найдем общее решение второго уравнения - функции U(x). А так как решение y(x)=UV, то, значит, мы нашли и его.
Пример 3. Найти общее решение линейного ДУ:  .
.
Решение.
Поделим уравнение на 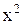 и перенесем слагаемое
и перенесем слагаемое  в правую часть:
в правую часть:

Следуя процедуре, изложенной выше, применим подстановку 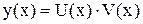 :
:


Уравнение распадается на два уравнения с разделяющимися переменными:



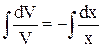 .
Находим какую-либо функцию V (все V здесь не нужны): .
Находим какую-либо функцию V (все V здесь не нужны):
 . Отсюда . Отсюда  Подставляем во второе уравнение
Подставляем во второе уравнение
| 




 ,
где С–произвольная постоянная. ,
где С–произвольная постоянная.
|
Окончательно получаем 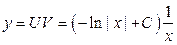 .
.
 2020-04-07
2020-04-07 107
107








