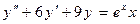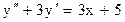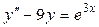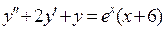Кафедра «Математика»
Методические указания
И варианты заданий для выполнения
Контрольной работы №2
По дисциплине «Математика»
Для студентов заочной формы обучения
Технических направлений
(нормативный и сокращенный срок обучения)
Ростов-на-Дону
2019
Составители: Ароева Г.А., Поляков А.С.
Контрольная работа №2 для студентов заочной формы обучения технических направлений – Ростов н/д: Издательский центр ДГТУ. 2019. – с.
Методическая разработка предназначена для студентов заочной формы обучения технических специальностей. Содержит программу курса математики по разделам: «Обыкновенные дифференциальные уравнения», «Ряды», «Теория вероятностей и математическая статистика». Указана рекомендуемая литература, варианты контрольной работы № 2 (второй семестр), а также даны образцы решения задач. В контрольной работе представлены задачи, содержащие десять вариантов. Вариант задания студент определяет по последней цифре номера зачетной книжки. Цифра 0 соответствует варианту 10.
Печатается по решению методической комиссии факультета «Информатика и вычислительная техника»
Рецензент: к.ф.-м.н., доц. Ворович Е.И. (ДГТУ, г. Ростов-на-Дону)
Научный редактор: к.ф.-м.н., доц. Волокитин Г.И.
© Издательский центр ДГТУ, 2019
Экзаменационная программа по математике
Для студентов 1-го (2 семестр) курса заочной формы обучения
Дифференциальные уравнения
Основные определения и понятия теории дифференциальных уравнений. Задача Коши для дифференциального уравнения первого порядка, геометрический смысл решения задачи Коши. Теорема существования и единственности решения задачи Коши. Основные типы дифференциальных уравнений первого порядка, интегрируемых в квадратурах. Дифференциальные уравнения второго порядка, допускающие понижение порядка. Линейные дифференциальные уравнения высших порядков. Структура общего решения линейного однородного и линейного неоднородного дифференциального уравнения. Линейные дифференциальные уравнения с постоянными коэффициентами, характеристическое уравнение. Нахождение частного решения методом неопределенных коэффициентов.
Ряды
Определение ряда. Геометрический и гармонический ряды. Необходимое условие сходимости ряда. Положительные ряды: критерий сходимости. Первый и второй признаки сравнения. Положительные ряды: признак Даламбера и радикальный признаки Коши. Положительные ряды: интегральный признак сходимости Коши. Обобщенный гармонический ряд. Знакочередующиеся ряды. Абсолютная и условная сходимость знакопеременных рядов. Теорема Лейбница и ее следствие. Понятие степенного ряда. Теорема Абеля, интервал сходимости, радиус сходимости степенного ряда. Основное свойство степенных рядов. Разложение функций в степенной ряд. Логарифмический ряд. Ряды Тэйлора. Разложение функции в степенной ряд: критерий представления функции степенным рядом, достаточные условия представления функции степенным рядом. Ряды Маклорена функций  .
.
Ряды Фурье. Понятие тригонометрического ряда. Определение ортогональных систем функций и тригонометрическая система функций. Формулы Эйлера-Фурье и определение ряда Фурье. Достаточные условия представимости функции с периодом T=2p ее рядом Фурье (теорема Дирихле). Ряд Фурье для четных и нечетных функций. Периодическое продолжение функций. Ряд Фурье в случае произвольного периода T=2l и ряд Фурье для функции, заданной на несимметричном интервале.
Теория вероятностей и математическая статистика
Основные понятия. Случайные события. Алгебраические операции над событиями. Множество элементарных событий. Алгебра событий. Аксиоматическое определение вероятности события. Вероятностное пространство.
Классическое определение вероятности события. Статистическое определение вероятности события. Геометрическое определение вероятности события. Свойства вероятности. Теоремы сложения вероятностей.
Элементы комбинаторики. Комбинаторный метод вычисления вероятностей в классической схеме.
Условная вероятность. Теорема умножения. Независимость событий.
Формула полной вероятности и формулы Байеса.
Схема независимых испытаний Бернулли. Формула Бернулли. Наивероятнейшее число появления события в независимых испытаниях. Предельные теоремы в схеме Бернулли. Формулы Муавра-Лапласа и Пуассона.
Случайные величины. Определение случайной величины. Дискретные случайные величины (ДСВ) и случайные величины непрерывного типа (СВНТ).
Задание дискретных случайных величин. Закон и функция распределения ДСВ.
Числовые характеристики ДСВ: математическое ожидание, дисперсия и другие моменты. Свойства математического ожидания и дисперсии.
Примеры ДСВ: гипергеометрическое распределение, биномиальное распределение, закон Пуассона.
Задание СВНТ. Функция распределения и функция плотности вероятностей. Свойства этих функций. Числовые характеристики непрерывных случайных величин. Примеры непрерывных распределений: равномерное, нормальное и показательное распределения.
Совместное распределение нескольких случайных величин. Функции случайных величин и их числовые характеристики. Независимость случайных величин. Ковариация, коэффициент корреляции. Закон больших чисел. Неравенство Чебышева. Теорема Чебышева. Предельные теоремы. Понятие о предельных теоремах. Центральная предельная теорема для суммы одинаково распределенных слагаемых. Теорема Ляпунова.
Выборка и способы ее представления. Числовые характеристики выборочного распределения.
Точечные оценки и их свойства. Статистическое оценивание характеристик распределения генеральной совокупности по выборке.
Интервальные оценки. Доверительный интервал, надежность и точность оценки. Доверительный интервал для центра нормального распределения при известной дисперсии. Доверительный интервал для среднего квадратичного отклонения нормального распределения.
Проверка статистических гипотез. Критерий согласия Пирсона.
Линейная регрессия. Элементы регрессионного анализа и метод наименьших квадратов. Характер связи и его оценивание по коэффициенту корреляции.
Литература
Основная
1. Н.С. Пискунов, Дифференциальное и интегральное исчисление. Том 1,2. 1972-2000.
2. А.Ф. Бермант, И.Г. Араманович. Краткий курс математического анализа для втузов. Москва: “Наука”. Главная редакция физико-математической литературы, 1973.
3. Г.М. Берман, Сборник задач по курсу математического анализа (для втузов). Москва: “Наука”. 1985.
4. П. Е. Данко, и др. Высшая математика в упражнениях и задачах: Учебное пособие для втузов. В 2-х ч. 1980 – ч.1, 1984 – ч.2.
5. Гмурман В. Е. Теория вероятностей и математическая статистика. - М.: Высшая школа, 1998.
6. Гмурман В. Е. Руководство к решению задач по теории вероятностей и математической статистике. – М: Высшая школа, 1999.
Дополнительная
1. Кремер Н. Ш. Теория вероятностей и математическая статистика. – М.: ЮНИТИ, 2000.
2. Вентцель Е. С. Теория вероятностей – М.: Высшая школа, 1998.
3. Учебные задания для типовых расчетов по теории вероятностей /ДГТУ. Ростов н/Д, 1996.
4. Сборник задач по математике для вузов Ч. З. Теория вероятностей и математическая статистика: Учебное пособие для втузов / Под редакцией А. В. Ефимова. – М.: Наука, 1990.
Задача 1. Найти общее решение дифференциального уравнения с разделяющимися переменными.
1. 
2. 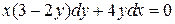
3. 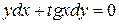
4. 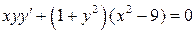
5. 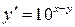
6. 
7. 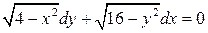
8. 
9. 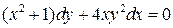
10. 
Задача 2. Найти общее решение однородного дифференциального уравнения.
1. 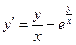
2. 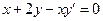
3. 
4. 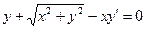
5. 
6. 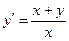
7. 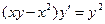
8. 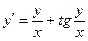
9. 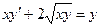
10. 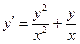
Задача 3. Найти, применяя подстановку Бернулли, общее решение линейного дифференциального уравнения первого порядка.
1. 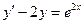
2. 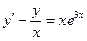
3. 
4. 
5. 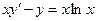
6. 
7. 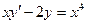
8. 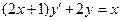
9. 
10. 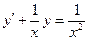
Задача 4. Найти общее решение линейного неоднородного уравнения второго порядка с постоянными коэффициентами.
10. 
Задача 5. Исследовать сходимость положительного ряда, применяя какой–либо из достаточных признаков сходимости (сравнения, Даламбера, радикальный или интегральный):
1. a) 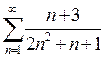 ; b)
; b)  ; c)
; c) 
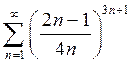 .
.
2. a)  ; b)
; b) 
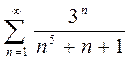 ; c)
; c) 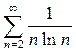 .
.
3. a)  ; b)
; b) 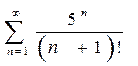 ; c)
; c)  .
.
4. a) 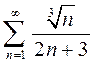 ; b)
; b)  ; c)
; c) 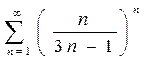 .
.
5. a)  ; b)
; b) 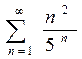 ; c)
; c)  .
.
6. a) 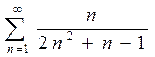 ; b)
; b) 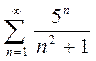 ; c)
; c) 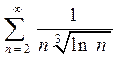 .
.
7. a)  ; b)
; b) 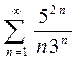 ; c)
; c)  .
.
8. a)  ; b)
; b) 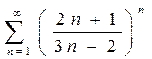 ; c)
; c)  .
.
9. a) 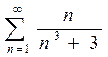 ; b)
; b) 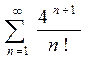 ; c)
; c)  .
.
10. a)  ; b)
; b) 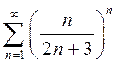 ; c)
; c) 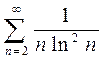
Задача 6. Найти интервал сходимости степенного ряда, исследовать его поведение на концах интервала сходимости и указать область сходимости:
 |
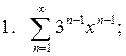
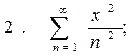
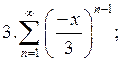

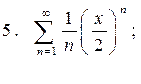
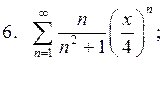



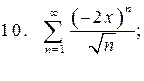
Задача 7. (Комбинаторный метод вычисления вероятностей в классической схеме).
1. В забеге участвуют 5 спортсменов: А, Б, В, Г, Д, каждый из которых имеет
одинаковые шансы на успех. Какова вероятность того, что первые три места займут соответственно бегуны А, Б, В?
2. В партии деталей 12 стандартных изделий и 3 нестандартных. 5 деталей, выбранных наудачу, проверяют на соответствие стандарту. Найти вероятность того, что среди них не окажется нестандартных.
3. На складе телевизионного ателье из имеющихся 20 микросхем 6 изготовлены первым заводом, остальные - вторым. Найти вероятность того, что две наудачу взятых микросхемы изготовлены первым заводом.
4. Участники жеребьевки тянут из ящика жетоны с номерами от 1 до 100. Найти вероятность того, что номер первого наудачу извлеченного жетона не содержит цифры 5.
5. Бросают две игральные кости. Определить вероятность того, что сумма числа очков не превосходит 7.
6. В группе 15 студентов, из которых 6 отличников. По списку наудачу отобраны 5 студентов. Найти вероятность того, что среди отобранных студентов нет отличников.
7. В магазин поступило 30 телевизоров. Из них 3 имеют скрытые дефекты. Покупателю для выбора наудачу предложено 2 телевизоров. Вероятность того, что все предложенные покупателю изделия не содержат дефектов?
8.Восемь различных книг расставляются рядом на одной полке. Найти вероятность того, что две определенные книги окажутся поставленными рядом.
9. Из колоды 36 карт наугад выбраны 3 карты. Какова вероятность, что среди их имеется хотя бы один «туз»?
10. Из партии, содержащей 10 изделий, среди которых 3 бракованных, наудачу извлекают 3 изделия для контроля. Тогда вероятность того, что в полученной выборке ровно 1 бракованное изделие.
Задача 8. (Формула полной вероятности и формула Байеса)
1. Для участия в студенческих спортивных соревнованиях выделено 12 человек из первой группы и 8 из второй. Вероятность того, что студент первой группы попадет в сборную института, равна 0,8, а для студента второй группы – 0,6.
а) Найти вероятность того, что случайно выбранный студент попал в сборную института. б) Студент попал в сборную института. В какой группе он вероятнее всего учится?
2. Детали попадают на обработку на один из трех станков с вероятностями, соответственно равными: 0,.2; 0,3; 0,5. Вероятность брака на первом станке равна 0,02; на втором – 0,03; на третьем – 0,01. Найти:
а) вероятность того, что случайно взятая после обработки наугад деталь – стандартная;
б) вероятность обработки наугад взятой детали на втором станке, если она оказалась стандартной.
3. Среди поступивших на сборку деталей 30% - с завода № 1, остальные – с завода № 2. Вероятность брака для завода № 1 равна 0,02, для завода № 2 – 0,03. Найти:
а) вероятность того, что наугад взятая деталь стандартная;
б) вероятность изготовления наугад взятой детали на заводе № 1, если она оказалась стандартной.
4. На сборку поступают детали с трех конвейеров. Первый дает 25%, второй – 30% и третий – 45% деталей, поступающих на сборку. С первого конвейера в среднем поступает 2% брака, со второго – 3%, с третьего – 1%. Найти вероятность того, что:
а) на сборку поступила бракованная деталь;
б) поступившая на сборку бракованная деталь – со второго конвейера.
5. Комплектовщик получает для сборки 30% деталей с завода № 1, 20% - с завода № 2, остальные – с завода № 3. Вероятность того, что деталь с завода № 1 – высшего качества, равна 0,9, для деталей с завода № 2 – 0,8, для деталей с завода № 3 – 0,6. Найти вероятность того, что:
а) случайно взятая деталь – высшего качества;
б) наугад взятая деталь высшего качества изготовлена на заводе № 2.
6. Заготовка может поступить для обработки на один из двух станков с вероятностями 0,4 и 0,6 соответственно. При обработке на первом станке вероятность брака составляет 2%, на втором – 3%. Найти вероятность того, что:
а) наугад взятое после обработки изделие – стандартное;
б) наугад взятое после обработки стандартное изделие обработано на первом станке.
7. На двух станках обрабатываются однотипные детали. Вероятность брака для станка № 1 составляет 0,03, для станка № 2 – 0,02. Обработанные детали складываются в одном месте, причем деталей, обработанных на станке № 1, вдвое больше, чем на станке № 2. Найти вероятность того, что:
а) взятая наугад деталь будет стандартной;
б) наугад взятая стандартная деталь изготовлена на первом станке.
8. В дисплейном классе имеется 10 персональных компьютеров первого типа и 15 второго типа. Вероятность того, что за время работы на компьютере первого типа не произойдет сбоя, равна 0,9, а на компьютере второго типа – 0,7. Найти вероятность того, что:
а) на случайно выбранном компьютере за время работы не произойдет сбоя;
б) компьютер, во время работы на котором не произошло сбоя, - первого типа.
9. В пяти ящиках с 30 шарами в каждом содержится по 5 красных шаров, в шести – по 4 красных шара. Найти вероятность того, что:
а) из наугад взятого ящика наудачу взятый шар будет красным;
б) наугад взятый красный шар содержится в одном из первых пяти ящиков.
10. По линии связи передано два сигнала типа А и В с вероятностями соответственно 0,8 и 0,2. В среднем принимается 60% сигналов типа А и 70% типа В. Найти вероятность того, что:
а) посланный сигнал будет принят;
б) принятый сигнал типа А.
Задание 9. Выборка, её числовые характеристики
Для указанных ниже статистических распределений выборок требуется:
1) Найти эмпирическую функцию распределения и построить ее график.
2) Построить полигон частот.
3) Вычислить выборочную среднюю.
4) Вычислить выборочную и исправленную дисперсии.
1. xi 1 4 8 10
ni 5 3 2 1
2. xi -5 1 3 5
ni 2 5 3 1
3. xi 1 5 9 11
ni 2 3 5 1
4. xi -2 1 2 3 4 5
ni 2 1 2 2 2 1
5. xi 0 1 2 3 4
ni 5 2 1 1 1
6. xi 1 5 6 8
ni 5 15 20 10
7. xi 1 5 7 9
ni 6 12 1 1
8. xi 2 3 5 6
ni 10 15 5 20
9. xi -5 2 3 4
ni 4 3 1 2
10. xi 1 2 4 7
ni 1 3 6 2
Задание 10. Доверительные интервалы для параметров нормального закона распределения
Найти доверительный интервал для оценки математического ожидания а нормального распределения с надежностью 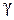 = 0,95, зная выборочную среднюю
= 0,95, зная выборочную среднюю 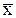 , объем выборки n и среднее квадратичное отклонение
, объем выборки n и среднее квадратичное отклонение 
1. 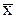 = 75,17; n = 36;
= 75,17; n = 36; 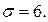
2. 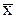 = 75,16; n = 49;
= 75,16; n = 49; 
3. 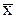 = 75,15; n = 64;
= 75,15; n = 64; 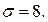
4. 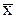 = 75,14; n = 81;
= 75,14; n = 81; 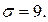
5. 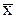 = 75,13; n = 100;
= 75,13; n = 100; 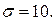
6. 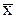 = 75,12; n = 121;
= 75,12; n = 121; 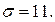
7. 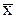 = 75,11; n = 144;
= 75,11; n = 144; 
8. 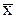 = 75,10; n = 169;
= 75,10; n = 169; 
9. 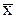 = 75,09; n = 196;
= 75,09; n = 196; 
10. 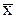 = 75,08; n = 225;
= 75,08; n = 225; 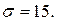
 2020-04-07
2020-04-07 221
221