2020-04-07
123
Задание 7. Классическое определение вероятности
Из 10 служащих туристического агентства 7 знают французский язык. Какова вероятность того, что среди трех человек, находящихся в данный момент в офисе, французским владеют двое?
Решение.
Число благоприятных исходов – это произведение количества способов, которыми можно выбрать двух человек, знающих французский язык, из семи, и способов, которыми можно выбрать одного человека, не знающего этого языка, из оставшихся трех.
, 
, 
.
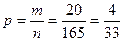Ответ: 
Задание 8. Формула полной вероятности и формулы Байеса
В первой урне 4 белых шара и 6 черных, во второй 1 белый и 9 черных, в третьей 10 черных шаров. Из наудачу выбранной урны вынут шар. Найти вероятность того, что он белый.
Решение.
Используем формулу полной вероятности, считая гипотезами выбор урны (все три гипотезы равновероятны). Пусть событие А – извлечение белого шара, гипотезы Н1, Н2, Н3 – выбор соответствующей урны. Тогда
, 
, 
,
.
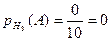Ответ: 
.
Задание 9. Выборка, её числовые характеристики
Дан закон распределения частот для дискретной случайной величины 
в виде следующей таблицы
| 1 | 2 | 4 | 7 |
| 1 | 3 | 6 | 2 |
Требуется найти: 1) эмпирическую функцию распределения; 2) полигон частот; 3) выборочную среднюю; 4) выборочную дисперсию; 5) исправленную дисперсию.
Решение.
1) Объем выборки равен сумме частот: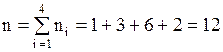 
. Эмпирическая функция 
, где 
– суммарное число выборочных значений тех частот, аргументы которых удовлетворяет неравенству 
. Поэтому функция 
равна:
а) 
; б) 
; в) 
; г) 
;
д) 
.
Рис.1 Эмпирическая функция распределения .
| 2) Построим полигон частот по данному распределению выборки в виде ломаной линии |
Рис. 2. Полигон частот
3) Найдем теперь выборочное среднее 
по следующей формуле
.
В данном случае число групп данных 
, поэтому выборочное среднее равно
.
4) Найдем теперь выборочную дисперсию по следующей формуле
.
Для упрощения вида числовых выкладок приближенно считаем, что 
, поэтому
.
5) Найдем теперь исправленную дисперсию по следующей формуле
.
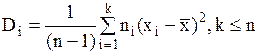Выводим для 
, что она равна
.
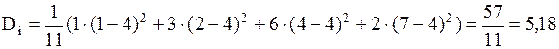Задание 10. Доверительные интервалы для параметров нормального закона распределения.
Найти с 
надежностью 
доверительный интервал оценки неизвестного математического ожидания 
для нормально распределенного признака 
, если даны значения: генеральное среднее квадратичное отклонение 
; выборочное среднее 
; объем выборки 
.
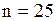Решение.
Неизвестное математическое ожидание находится в интервале
.
Последняя в записи формула обозначает уравнение относительно t, содержащее функцию Лапласа 
:
,
Применяя таблицы функции Лапласа, находим неизвестное значение параметра 
. Определим величину 
.
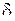
Найдем доверительный интервал
.
Доверительный интервал 
покрывает математическое ожидание для нормально распределенной случайной величины с заданной величиной надежности 
, которая называется также доверительной вероятностью. В данной задаче доверительная вероятность равна 0,99 или 99%.
